Noticed this at meander lawn who has a really broad puzzle blogroll… I don’t really know what I’m doing and may have misinterpreted something, but here goes. (Ahahaha puzzle 33 on 11/22… I wish it was intentional :P)
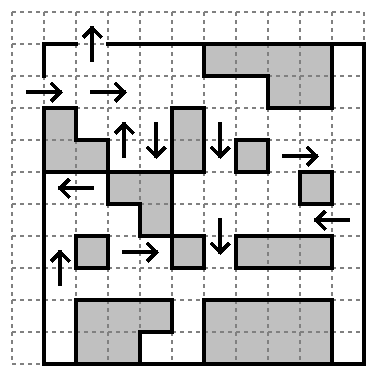
Draw a path through square centers which enters and exits through the given places. Outside the “ice barns” (the gray things), the path may turn freely but may not self-intersect; inside “ice barns” the path may self-intersect but may not turn. Each ice barn (not necessarily every cell but every region, I think) must be passed over. The path must pass through each given arrow in the given direction.
For absolutely no good reason whatsoever, I would like to announce that somebody has found this blog with the search query [given triangle abc the point j is the centre of the excircle opposite the vertex a.this excircle is tangent to the side bc at m, and to the lines ab and ac at k and l, respectively.the lines lm and bj meet at f, and the lines km and cj meet at g. let s be the point ofintersection of the lines af and bc, and let t be the point of intersection of the lines ag and bc.prove that m is the midpoint of st.]
Also, [metal chopsticks taste like metal]. Think about it. Have your mind blown.