JS Safe 2.0

You stumbled upon someone’s “JS Safe” on the web. It’s a simple HTML file that can store secrets in the browser’s localStorage. This means that you won’t be able to extract any secret from it (the secrets are on the computer of the owner), but it looks like it was hand-crafted to work only with the password of the owner…

The challenge consists of a fancy HTML file with a cute but irrelevant animated cube and some embedded JavaScript.

Seriously, though, since when can you create a spinning 3D cube in your browser with only a few lines of CSS and HTML. I am behind on front-end technology.

Above the cube there’s a simple <input> element with a cute “key” Unicode character. You can enter a random password into the box and watch your access get denied.

The onchange event handler of the <input> element is where everything begins:

<input id="keyhole" autofocus onchange="open_safe()" placeholder="🔑">

function open_safe() {
  keyhole.disabled = true;
  password = /^CTF{([0-9a-zA-Z_@!?-]+)}$/.exec(keyhole.value);
  if (!password || !x(password[1])) return document.body.className = 'denied';
  document.body.className = 'granted';
  password = Array.from(password[1]).map(c => c.charCodeAt());
  encrypted = JSON.parse(localStorage.content || '');
  content.value = encrypted.map((c,i) => c ^ password[i % password.length]).map(String.fromCharCode).join('')
}

For the challenge, the only relevant part of the on_safe function is that the safe will unlock if the password matches the regular expression /^CTF{([0-9a-zA-Z_@!?-]+)}$/ and the function call x(password[1]) is truthy. The rest of the code just decrypts the encrypted secret, which we don’t have since it’s on the safe owner’s localStorage. The regex is unremarkable, so we turn to the function x. It’s somewhat obfuscated by being all jammed into one line plus a few other gotchas we’ll see later, but it also declares a few friendly variable names that make the conversion between characters and their codepoints more familiar if you’re coming from Python. A lightly deobfuscated and commented version of the code is below:

function x(х){
    ord = Function.prototype.call.bind(''.charCodeAt);
    chr = String.fromCharCode;
    str = String;
    function h(s) {
        // Simple hash function that converts an arbitrary nonempty
        // string to a length-4 string of characters, each of which
        // has codepoint < 256.
        for (i = 0; i != s.length; i++) {
            a = ((typeof a == 'undefined' ? 1 : a) + ord(str(s[i]))) % 65521;
            b = ((typeof b == 'undefined' ? 0 : b) + a) % 65521;
        }
        return chr(b>>8) + chr(b&0xFF) + chr(a>>8) + chr(a&0xFF);
    }
    function c(a, b, c){
        // xors strings a and b together, cycling b as necessary to the
        // length of a (the third argument is never passed to this 
        // function and is just a mild obfuscation or code golf technique 
        // to introduce an extra local variable for "free")
        for (i = 0; i != a.length; i++)
            c = (c || '') + chr(ord(str(a[i])) ^ ord(str(b[i % b.length])));
        return c
    }
    // trigger the browser debugger to annoy anybody with their
    // browser developer tools open.
    for (a=0; a!=1000; a++) debugger;
    x = h(str(x));
    // what??
    source = /Ӈ#7ùª9¨M¤ŸÀ.áÔ¥6¦¨¹.ÿÓÂ.։£JºÓ¹WþʖmãÖÚG¤…¢dÈ9&òªћ#³­1᧨/;
    source.toString = function() {
        return c(source,x);
    };
    try {
        console.log('debug', source);
        with (source)
            return eval('eval(c(source,x))');
    } catch (e) {
        // swallow all errors
    }
    // implicitly return undefined (which is falsy)
}

There are three bamboozles in this function. The first bamboozle is in how source, a rather ugly regular expression, gets converted to a string. Following the code, source.toString calls c(source, x), which calls str on its first argument, which calls String on that argument, which calls the .toString() method on that argument, creating an infinite recursion. In fact, if you try to call source.toString() from the debugger or by manually inserting it, you will indeed cause infinite recursion and your browser will complain. And yet, the x function runs fine, even though it seems to evaluate c(source, x), which should enter the above infinite recursion.

The reason the loop isn’t entered is due to the (rare and disrecommended) with (source) statement. Any unqualified names (names that aren’t accessed by . from something else) inside a with statement will first be looked up as a property of the expression in parentheses after with. So, when the browser evaluates the unqualified variable source in 'eval(c(source,x))', it will first try to look up the source property of the regex that was provided to the with statement (and is also confusingly called source) before it tries anything else. Lo and behold, it just so happens that JavaScript regular expressions have an attribute source that contains the string of their, well, source. Since the browser finds this property, it decides that that’s what source in the with statement refers to, and the regex-that-was-also-called-source and its toString method are no longer relevant.

In any case, on a high level, the function x hashes its input to get a length-4 key, xors it with the body text of the regex, and evaluates the resulting string as JavaScript. We want this evaluation to succeed (notably, it has to be syntactically correct JavaScript) and return a truthy value.

(If you solved the challenge, you will know that the above description is technically inaccurate because of the second bamboozle, but it is completely possible to finish this stage without realizing the inaccuracy, and it’s how I did it, so I will stick to this narrative.)

There are 65521² possible hashes, which is basically 2³². If checking each hash were easy, this would be within brute-force reach, but evaluating a piece of JavaScript is expensive. Instead the best way is probably to use some smart intuition and wild guessing.

The first thing to do is to extract the exact sequence of code points from the regex exactly as it appears on the page, partly so we can stop worrying about encodings getting us into trouble and partly just to see the characters:

This gives the list:

1223, 35, 55, 249, 170, 57, 168, 77, 164, 159, 192, 46, 225, 212, 165, 54, 166, 168, 185, 46, 255, 211, 194, 46, 214, 137, 163, 74, 186, 211, 185, 87, 254, 202, 150, 109, 227, 214, 218, 71, 164, 133, 162, 100, 200, 57, 38, 242, 170, 1115, 35, 179, 173, 49, 6632

Surprisingly, the codepoints include two numbers over 1000 and one over 6000 (bolded), but the hash that we will xor it with only includes bytes up to 256, so there is no way for these code points to get xored into ASCII characters.

In fact, we can conclude that no matter what the xor key is, the last character will appear exactly once in this code snippet. We can then make the intuitive leap that the easiest way for this to be valid and remotely reasonable JavaScript is for it to be commented out. (There are of course other ways. By choosing a byte, we can make this codepoint xor to a character from one of the Unicode blocks Tagalog, Hanunoo, Buhid, Tagbanwa, or Khmer, many of which are valid Unicode letters and could be used as JavaScript identifiers or parts thereof. Then if we accessed this identifier, we’d just get undefined. But that would be pretty inelegant, so let’s run with this one.)

We can therefore guess that the first two bytes of the xor key are the bytes needed to make 173 and 49 xor to two forward slashes that will comment it out. To facilitate this checking process, I made a quick Google Sheet to automatically xor the code points with a number of my choice. This was harder than expected because apparently Google Sheets does not have the binary xor operator, so after more Googling for the answer I had to write a JavaScript function to implement this, and then call the function from the sheet.

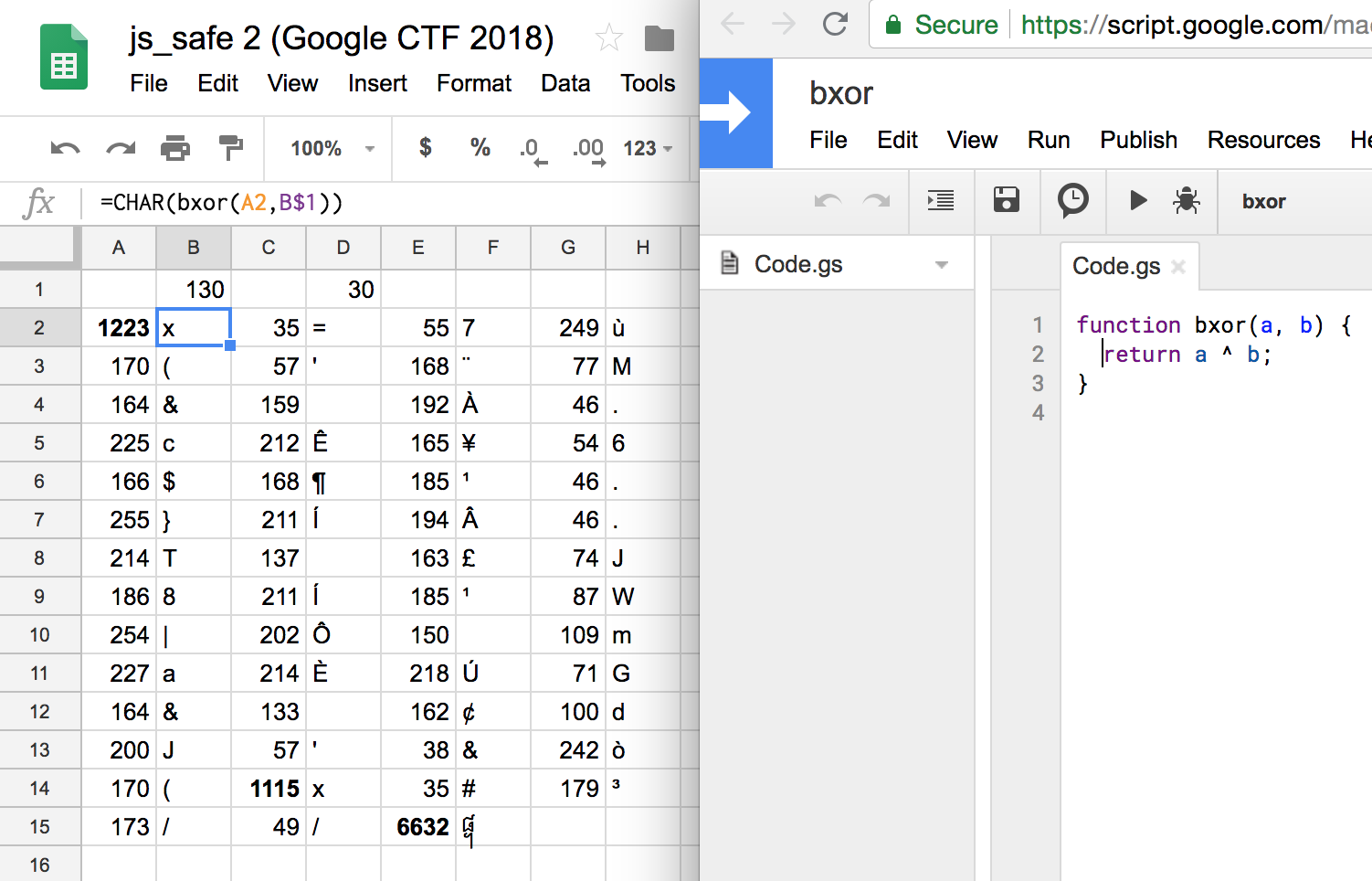
Promisingly, this makes the first two character xor to 1093 and 61, which are х and =, while it makes the sixth and seventh from last characters xor to 40 and 1093, which are ( and х. So the other two large codepoints turn into the same character х, which makes the JavaScript much more reasonable.

Still, this х should make you suspicious. Didn’t we just conclude that, as the xor of something over 1000 and something under 256, this character can’t be an ASCII character? Well, indeed, it is not; it is U+0445 CYRILLIC SMALL LETTER HA, one of those Latin character look-alikes that can be used for homograph spoofing attacks. And indeed, the second bamboozle of this challenge is that we’ve been tricked by a spoofing attack all along: although the function we’ve been analyzing this whole time is called x, or U+0078 LATIN SMALL LETTER X, its parameter is called U+0445 CYRILLIC SMALL LETTER HA.

This means that the line

x = h(str(x));

(in which both x’s are the Latin x) is actually converting the function itself to a string. And JavaScript functions’ toString basically return the function’s source code, whitespace, comments, and all.¹ This means that any deobfuscation of the function will change its hash and its behavior and cause the check to fail, even if you enter the right key. Whoops.

All this means that the value of (the Latin) x that we xor with source doesn’t depend on the password we type at all! So we can extract the result of c(source, x) by logging it after copy-pasting the relevant definitions from x outside. Doing this correctly also requires you to realize the third bamboozle, which is that even outside the function x you can’t ignore the annoying loop for (a=0; a!=1000; a++) debugger;. The reason is that it sets a to 1000, and afterwards the hash function uses the variable a without declaring it in an inner scope. So despite appearances, the “initialization clause” in the line

a = ((typeof a == 'undefined' ? 1 : a) + ord(str(s[i]))) % 65521;

that purports to default a to 1 the first time through the loop never happens, because a is already set to 1000. (The same clause for b does occur, of course.)

The end result is that this code, with some functions copy-pasted verbatim from the challenge file, will give you the correct string:

function x(х){/* copy-paste */}
a = 1000;
ord = Function.prototype.call.bind(''.charCodeAt);
chr = String.fromCharCode;
str = String;
function h(s){/* copy-paste */}
function c(a,b,c){/* copy-paste */}
source = /Ӈ#7ùª9¨M¤ŸÀ.áÔ¥6¦¨¹.ÿÓÂ.։£JºÓ¹WþʖmãÖÚG¤…¢dÈ9&òªћ#³­1᧨/;
console.log(c(source.source, h(x.toString())));

Alternatively, if you are like me and somehow still failed to realize that c(source, x) doesn’t depend on the password even after discovering the homograph substitution, you can continue deducing the hash along the same lines. It’s actually doable, and guessing is fun! The seventh-to-last character is an open parenthesis, so it should likely be closed. So we set the other two characters of the xor key to the values that would cause the fourth- and fifth-to-last characters to be close parentheses, with the goal of seeing if either of these produce a promising column. It turns out that in fact both of them together produce a syntactically correct and very promising piece of code. That was easy. Of course, it would have been even easier for anybody who realized that one of the х’s in the code was Cyrillic earlier.

Either way, we conclude that c(source, x) gives the following line of code, which has to evaluate to true:

х==c('¢×&Ê´cʯ¬$¶³´}ÍÈ´T—©Ð8ͳÍ|Ԝ÷aÈÐÝ&›¨þJ',h(х))//᧢

As noted before, the х above is the Cyrillic lookalike for x, and it actually refers to the argument to the Latin-letter-x function, which is just the text between CTF{ and } in the safe password. For this to be true, х has to be the result of xoring a key with the “ciphertext” '¢×&Ê´cʯ¬$¶³´}ÍÈ´T—©Ð8ͳÍ|Ԝ÷aÈÐÝ&›¨þJ'. But we also know from the open_safe function that х has to match the regex /[0-9a-zA-Z_@!?-]+/. This is easy to brute force. For each character in the xor key, it must xor with roughly one-fourth of the characters in that string to create a character from the relatively small character class of the regex, which is a pretty strong constraint.

A short Python script will finish the challenge:

import re
xored_string = '¢×&Ê´cʯ¬$¶³´}ÍÈ´T—©Ð8ͳÍ|Ԝ÷aÈÐÝ&›¨þJ'

valid_key_codepoints = [[],[],[],[]]
for i in range(4):
    for key_cp in range(256):
        good = True
        for c in xored_string[i::4]:
            if not re.match('[0-9a-zA-Z_@!?-]+', chr(ord(c) ^ key_cp)):
                good = False
                break
        if good:
            valid_key_codepoints[i].append(key_cp)
print(ks)

This works in Python 3; in Python 2, to get the right codepoints out, you need to add # coding: utf-8 to the start and prefix the string literal with u to declare that it’s a Unicode string. Or, in either language, you can just parse the codepoints out in JavaScript and paste them in like so:

xored_string = ''.join(map(chr, [
    162, 215, 38, 129, 202, 180, 99, 202
    175, 172, 36, 182, 179, 180, 125, 205
    200, 180, 84, 151, 169, 208, 56, 205
    179, 205, 124, 212, 156, 247, 97, 200
    208, 221, 38, 155, 168, 254, 74
]))

You could equivalently do the above procedure with the string sliced from the original source’s source’s source that turned into this string, since that transformation was also via xoring a period-4 key, and xoring by two different period-4 keys is equivalent to xoring by the xor of those keys.

Anyway, the Python script prints:

[[253], [149, 153], [21], [249]]

So we know the first, third, and fourth characters of the xor key, and there are only two possibilities for the second. In other words, the regex alone has reduced our space of 65536 possible xor keys to just two. Trying the second one produces the text _N3x7-v3R51ON-h45-AnTI-4NTi-ant1-D3bUg_, which sure looks like a flag, and it grants access after we surround it with CTF{ ... }:

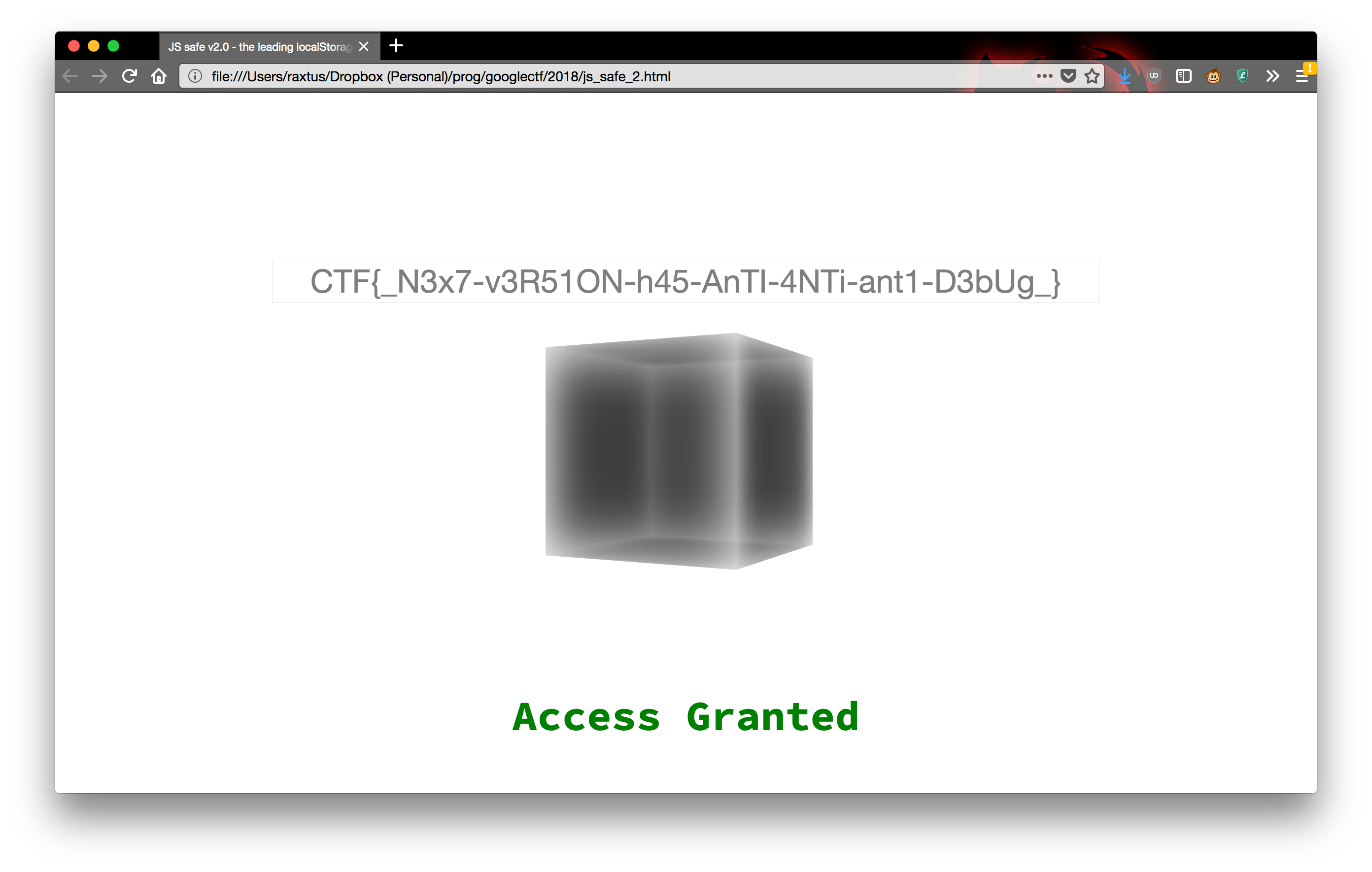
So the flag is:

CTF{_N3x7-v3R51ON-h45-AnTI-4NTi-ant1-D3bUg_}

Incidentally, this challenge leaves an interesting question of how the function and the flag were written. The ciphertext is a pure function of the flag, but the hash that the regex source is xored with to create the ciphertext depends on the source itself, which contains the regex source; so how do you get it to produce the ciphertext? The haphazard capitalization and 1337ification of the flag makes me think various ways to choose the uppercase, lowercase, or 1337speak versions of individual characters of the flag were bruteforced along with valid xor keys until the result of embedding the ciphertext in the expression, xoring with the xor key, and then embedding that as a regex in the function source happened to hash to the xor key. The hash function is naive enough that this can made pretty fast if you perform some precomputations with the parts of the function source that are fixed. I’m not sure whether some way to find a flag that works even more efficiently would fall out if you just write out all the math, though.