After the first stage of selection camp, I was very nervous because I was fifth place in a selection sequence that would finally result in a team of four.
I screwed myself over on the first mock test by committing to a bad implementation method on a problem that was hard to get points on. My method seemed simple, but the memory usage leaked out in a way that was confusing and hard to patch; unfortunately, I tried to patch it in increasingly desperate and convoluted ways rather than scrapping the method, and thus missed out on many of the points elsewhere.
During the second test I failed to read the last problem carefully and spent too much of my time on the second problem, once again missing out on a lot of relatively easy points. I had optimized and optimized and pushed my quadratic runtime down to linearithmic, which would allow me to get the points for the last subtask — or so I thought. But with 10 minutes left I had all but one testcase right, and after desperately rereading my code, I realized that I had a string comparison stuck in an inner loop that could make my runtime degenerate to quadratic if the input string had lots of the same digit. In order to have a solidly linearithmic algorithm, I would have to implement a suffix array. Ten minutes? I gave up. (The problem setters told me afterwards that hashing would have worked too; I didn’t think of that at all. Oops.) I spent the 10 minutes reading the last problem and still failed to read it carefully. So that did not go very well.
But, as the title probably gave away, during the third and fourth mock tests everything went much better than expected. :)
There are two good reasons:
- I had finally learned that in these mock tests, the correlation between problem position and difficulty was effectively zero. This is true even if you assume “difficulty” refers to “difficulty according to a rushed problem-setting committee who only has time to judge a problem by how complex its solution looks rather than how hard it is to think of the solution.” Long-term readers of this blog know what IMO problem I’m referring to. Knowing this changed my score-maximization strategy significantly.
- The later test problems had more math-olympiad dependencies, and were thus naturally immensely advantageous for myself too.
To elaborate: Test #3 included one strange output-only hodgepodge problem of probability and combinatorial design tasks, and one combinatorial enumeration problem involving the Fibonacci sequence which then required some optimizations with number theory. Test #4 included two geometric problems, one somewhat standard and one somewhat “creative” (the last test case was a height map of Taiwan with our four nuclear power plants labeled.) Of course, since geometry on computers is always coordinate geometry, there was plenty of algebra in those problems too. So, in other words, these two tests pretty much covered all four math olympiad subject fields (otherwise known as silver cyanide) between them.
The story of problem 4.3 is so exciting that I’m going to tell it here. If geometry and estimates of asymptotic time complexity are not your sort of thing, you probably want to skip to the end of this post. There’s a mysterious fun animated bar graph there.
Problem 4.3, the un-story-fied version:
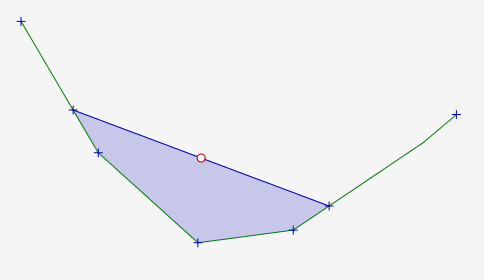
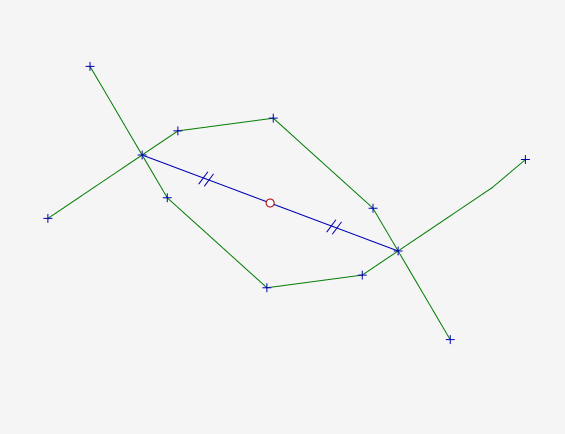
There’s an infinite convex polygonal line of N points, given to you with the coordinates of the points. Rigorously: there are at least 3 points, their x-coordinates strictly increase, and the slopes of the segments connecting each point to the next strictly increase as well. The first and last segments given are to be extended infinitely to the left and right. There’s also a “central point” specified above this polygonal line. Find the minimum possible area bounded by some line passing through the central point and the polygonal line.
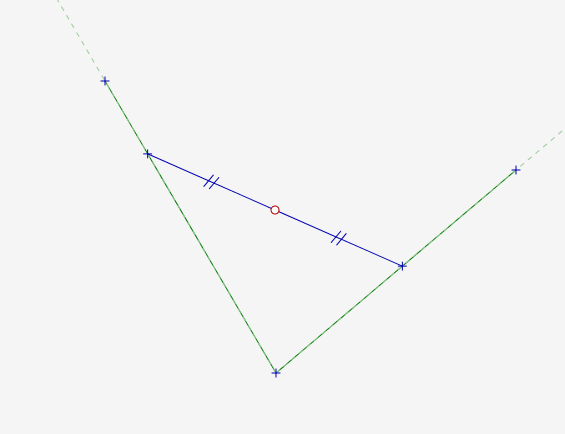
I drew a crappy freehand diagram and came up with the neat synthetic property hidden in the problem requirement: The central point had to be equidistant from the solution line’s intersections with the polygonal line.
The reason is that that’s where marginal benefit equals marginal cost. If you rotate the line a little dθ one way or the other, the change in area will be proportional to the square of the ratio of the distances from the central point to the places where the cut line intersects the polygonal line. Law of sines, vertical angles, economics 101. Boom!
Good job, me from the past.
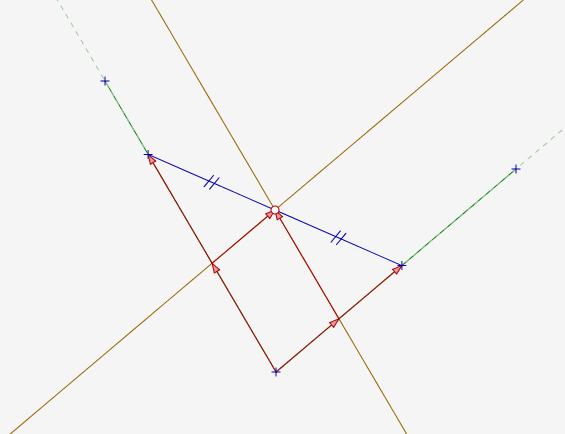
So obviously, I thought, the simplest way to calculate the right intersections given a polygonal line with only two segments was to construct a linear transformation mapping base unit vectors to the two segments’ displacements, and then applying its inverse to the displacement of the central point from the two segments’ intersection.
omgwtfbbq are you doing, me from the past.
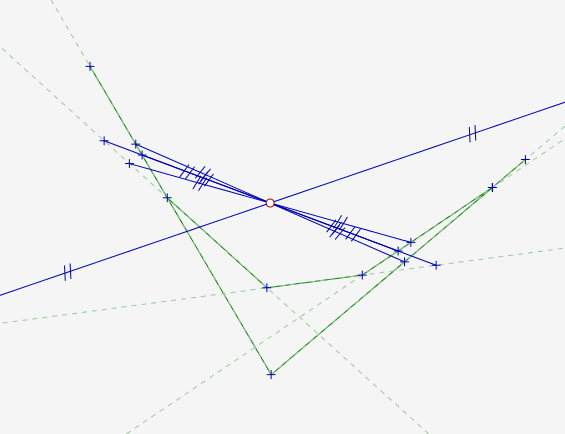
After discovering that, being the brilliant geometric impostor that I am, I decided to just check all \(\binom{n}{2}\) pairs by extending them, solving them as above, and checking if the answers were inside the actual segments, resulting in an at-least-quadratic-time brute-force.
(Sorry, I didn’t draw all Θ(n2) pairs above; I have time, but not that much time.)
This solved the first two subtasks, so I proceeded to bash the third by pretending it was “almost” monotonic. Intuitively I thought it was monotonic and the bruteforcing could be made linear by a two-pointer sweep, but after messing with it a little bit, I didn’t quite get it working and lacked the geometric finesse to figure out why. So I just brute-forced a bunch of extra combinations past the second pointer.
The results:
- With monotonic-plus-200, I had all the test data except one Wrong Answer.
- With monotonic-plus-320, I had all the test data except one Time Limit Exceeded.
I was about to give up and switch to making up solutions for Problem 4, until I backtracked on a faint suspicion and realized that the Wrong Answer and the Time Limit Exceeded were on different testcases.
So I set the magic number to 260 and got a mostly undeserved 25/25! Hooray! (This was only somewhat overshadowed by the fact that my score at that point was already enough to guarantee me a spot on the team, as long as our unofficial scores were accurate.)
The wallbash-worthy thing, which I learned after the contest, was of course that the intended solution was much simpler, eliminating the need for any linear transformation magic as well as any concerns about brute force and monotonicity in one fell swoop. And I was so close, too.
All that was necessary was to reflect the polygonal line about the central point.
Hindsight facepalm: in any synthetic geometry configuration, that midpoint should have been an immediate trigger for applying one of a long list of geometric transformations and auxiliary lines. I had completely forgotten about those triggers, probably because I never expected to use them again and I had replaced them with a few programming-competition triggers that had to almost always fire. So far, I only have two:
- “Binary search the answer!” (This helped in Test #2, actually.)
- “Use a scan line!”
Oops.
Maybe I’m just not very good at lines rotating around points… (Yes, that’s a link to the same problem.)
And so it ends. Or is it a beginning? I made it. I’m going to the 2014 International Olympiad in Informatics. There are several consequences.
- We get to take a plane to… oh wait, we’re staying in our own country. I know people in my place who’d rather travel to someplace exotic, go on cool excursions, and get some notable souvenirs. But I’m not a travel sort of guy; I actually prefer the home advantage.
- I might meet some more cool people! I don’t know. Have I matured enough to stop short-circuiting into socially-awkward-penguin mode around other people? To hell with that. I’m a dragon. Dragons don’t suffer from social anxiety because everybody is potential prey. Fake it ’til you make it.
- There’s probably going to be an [IOI 2014] tag and sequence of posts on this blog. Actually, let me commit to this beforehand so my future self doesn’t succumb to laziness and rationalize it away by finding a loophole: there will be an [IOI 2014] tag and sequence of posts on this blog. Take that, akrasia. (Admittedly, the tag already exists on this post, so half of that is already finished.)
- This is all very tentative, but I think this is going to be my last high-school olympiad, because alas, high-school is still too short for some things.
It’s too early to get carried away, though, because there’s another beast to slay before then. Four more, in fact, that I can think of right now, which all begin with “AP”:
- AP Microeconomics
- AP Macroeconomics
- AP English Language and Composition
- APIO (Asian Pacific Informatics Olympiad)
Haha.
Yes, okay, fine, I should be studying or practicing. As usual.
Post-script:
- Yes, the title of the post is somewhere between obnoxiously hyperbolic and confusingly irrelevant. For topics like this, that’s just how we roll.
- I didn’t post this yesterday when the news came out (well, that was fast) because I wasn’t finished writing it and because one of my HabitRPG dailies is “Go to sleep on time”, where “on time” means 10:30 PM. Seriously, it works. I’m Level 4 already.
- Oh, you were looking for the mysterious fun animated bar graph? Make sure to click the radio buttons. It’s my way of celebrating, I guess — grabbing a random popular library and cobbling pieces of code from the internet together until I get something that might pass for cool. It might even have something to do with this post. I wonder what…