This is a Fillomino puzzle where every polyomino is required to be an L-shape, as in Sashigane. Write a number in every empty cell so that every group of cells with the same number that is connected through its edges is an L-shape (with arms of positive length and 1-cell thickness) with that number of cells.

My second, and now symmetric, attempt at this crazy self-invented mutant; puzzle 22 was the first. A word of warning: I can’t solve this without bifurcating near the end, so logic purists may be disappointed, but I like the clue arrangement too much. In fact I suspect this puzzle could have many more clues removed without affecting uniqueness, so tight are the rule constraints in this type.

This is a Fillomino puzzle where every polyomino is required to be an L-shape, as in Sashigane. Write a number in every empty cell so that every group of cells with the same number that is connected through its edges is an L-shape (with arms of positive length and 1-cell thickness) with that number of cells.

May be slightly reminiscent of no-rectangle Fillominoes. Slightly… (Has anybody done this before? It seems so interesting that I feel like I couldn’t be first.)

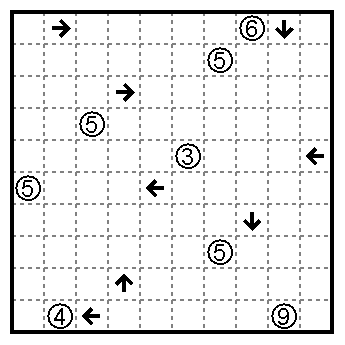
Yeah, I lied last time I made one of these; the original Nikoli name wasn’t that hard to remember, and “sashigane puzzles” has shown up as a search query, so here you go. Perfect opposite-type-clue rotational symmetry, chaotic_iak! I hope you’re satisfied now.

If you are reading this, then our APMO testing time is over! There’s a small chance of me being really happy or really frustrated about how I did, but I’m betting on a solid “meh.”

Rules page by mathgrant. There’s no way I’m going to memorize the Japanese name yet. [edit: It’s Sashigane. It’s not that hard.]