Designing a Programming Language to Speedrun Advent of Code

The title is clickbait. I did not design and implement a programming language for the sole or even primary purpose of leaderboarding on Advent of Code. It just turned out that the programming language I was working on fit the task remarkably well.

I can’t name just a single reason I started work on my language, Noulith, back in July 2022, but I think the biggest one was even more absurdly niche: I solve and write a lot of puzzlehunts, and I wanted a better programming language to use to search word lists for words satisfying unusual constraints, such as, “Find all ten-letter words that contain each of the letters A, B, and C exactly once and that have the ninth letter K.”¹ I have a folder of ten-line scripts of this kind, mostly Python, and I thought there was surely a better way to do this. Not necessarily faster — there is obviously no way I could save time on net by optimizing this process. But, for example, I wanted to be able to easily share these programs such that others could run them. I had a positive experience in this with my slightly older golflang Paradoc, which I had compiled into a WASM blob and put online and, just once, experienced the convenience of sharing a short text processing program through a link. (Puzzle: what does this program do?) I also wanted to write and run these programs while booted into a different operating system, using a different computer, or just on my phone.

As I worked on it, I kept accumulating reasons to keep going. There were other contexts where I wanted to quickly code a combinatorial brute force that was annoying to write in other languages; a glib phrasing is that I wanted access to Haskell’s list monad in a sloppier language. I also wanted an excuse to read Crafting Interpreters more thoroughly. But sometimes I think the best characterization for what developing the language “felt like” was that I had been possessed by a supernatural creature — say, the dragon from the Dragon Book. I spent every spare minute thinking about language features and next implementation steps, because I had to.

The first “real program” I wrote in Noulith was to brute force constructions for The Cube, for last year’s Galactic Puzzle Hunt in early August, and it worked unexpectedly well. I wrote a for loop with a 53-clause iteratee and the interpreter executed it smoothly. Eventually I realized that the language could expand into other niches in my life where I wanted a scripting language. For example, I did a few Cryptopals challenges in them. It would take a month or two before it dawned on me that the same compulsion that drove me to create this language would drive me to do Advent of Code in it. That’s just how it has to be.

This post details my thought process behind the design of this language. Some preliminary notes:

• I made a lot of unusual choices with this language, but none are particularly “deep” language features like Rust’s ownership checker, Mercury’s determinism checks and Pony’s reference guarantees (three examples lifted verbatim from “So You’re Using a Weird Language”). The immutability semantics are a little interesting, but still don’t have as far-reaching implications. To the extent the language breaks any new ground, it’s probably the boundaries of taste in adding syntax sugar. Still, syntax is fun.
• A lot of the decisions I made are deeply entangled with each other. I sort of try to string them together into a linear narrative for presentation’s sake, often also pretending that I researched how a bunch of other languages approached the same decision before making it myself, but the existence of such a narrative is mostly fictitious.
• Pixel’s syntax across languages page was immensely useful.
• Noulith was intended as a personal programming language first and foremost, deeply informed by and optimized for how I, specifically, think about and write code. I think of it as a “home-cooked” programming language, a la Robin Sloan’s home-cooked app. I did not create this language with the expectation or hope that even a single other person in the world would want to learn it; the amount of interest it briefly garnered was a (mostly) pleasant surprise. I also did not intend for this programming language to work well for programs that are longer than 100 lines or so, even if written by me. My best-case scenario is if one of the weird syntax experiments I did with this language vaguely influences a better thought-out feature in a major programming language.

• There are two concepts from interface design, internal consistency and external consistency, that are pretty obvious in hindsight but that I found useful to explicitly refer to below. Internal consistency refers to similar things within a single application working in similar ways, whereas external consistency refers to things in one application that are similar to things in other applications working in similar ways. Both are desirable since they make it easier to learn how to use the application: internal consistency means that users can learn things from one part of your application and apply them to another, while external consistency means that users can apply knowledge they might already have from other applications. But they can come into conflict with each other and with other desiderata.

  So for example, internal consistency favors giving two built-in functions to append and prepend an item to a list names that are clearly related, so programmers who remember one can easily remember the other; while external consistency favors copying those names from an established programming language if possible, so programmers coming from that established language already know those names.

  All this is relevant because of the sometimes underappreciated consideration that a programming language is a user interface! I think this perspective is easy to lose sight of because “programmers” and “users” are usually different groups of people, but for a programming language, the user is the programmer writing code in it, distinct from the programmer implementing the language.

• This post is too long — to quote the Mark Twain apology, I didn’t have time to write a short one — and as I finished it I realized that half of its raison d’être is just to provide an excuse for me to incidentally mention a bunch of interesting features and corner cases of other programming languages. So if you’d rather just read that, I collected most of the fun facts into an ending section.

Literals, identifiers, and data types

First things first. On a character-to-character, token-to-token level, what does the language look like?

There are a lot of questions that are too basic to be interesting, such as what numeric and string literals look like. This doesn’t have much impact on the rest of the language, so I just copied a bunch of popular syntaxes. For numbers, other than the obvious decimal ones, I threw in binary 0b literals, hexadecimal 0x literals, arbitrary radix 36r1000 literals, scientific notation 1e100 literals, and complex number 1i or 1j literals. I even added base64 literals for kicks. Strings can use either single or double quotes, essentially what Python has. Were I to add, say, ternary literals, additional flavors of triple-quoted or raw strings, or a bunch of special escape sequences, nothing else would have to change and there would be nothing to say about their design.

Identifiers have a bit more depth. Like most languages, most Noulith identifiers consist of a letter (including _) followed by any number of alphanumeric characters. From Haskell I copied the ability for such identifiers to also contain (but not start with) apostrophes, which I think looks neat for denoting a new version or modified variant of a variable, like the prime symbol in math. Much more questionably, I also gave ? the same treatment, with the goal of connoting variants of functions that returned null instead of erroring. In hindsight, I should perhaps not have muddled up the lexical syntax so much; a different convention, like a trailing _ on alphanumeric identifiers, might have sufficed. Separately, Noulith supports identifiers consisting of only symbolic characters as well, also like in Haskell. We’ll discuss how the parser treats them later.

I also had to think about the basic data types we want to support, but before that I had to decide if Noulith would be statically or dynamically typed. I like static types, but only if they’re sufficiently expressive and supported by good inference, and I like not having to implement any of that stuff even more, so I settled for dynamic typing.

I won’t list all the data types I ended up with here, but some of the basic ones are null, numbers, strings, lists, and dictionaries. Though null has a justifiably bad reputation, it’s hard to avoid in a dynamically typed language; it’s too useful as, for example, the return value of functions that don’t explicitly return anything. Notable omissions are booleans, sets, and any kind of dedicated error/exception type. I don’t think they are bad things to have in a language, I just thought they were significantly easier to work around than to implement, and I couldn’t be bothered to put in the work:

• Instead of true and false, you can just use numbers 0 and 1, which is close to how C and Python do it.
• Instead of sets, you can just use dictionaries where the values are null, so {a} == {a: null}. This still works well because in can just test for the presence of the key in a dictionary, a behavior also exactly like Python.
• Instead of dedicated error types, you can just use… non-dedicated data types. You can compose a string with an error message and throw it. I don’t like this state of affairs — I think having dedicated or at least more structured error types really is a good idea, maybe purely for the principle of the thing, but design and implementation both take effort, and it’s hard to argue for prioritizing this when I only use Noulith for short throwaway scripts.

I did not think hard about any these decisions, but they had consequences we’ll discuss later. For the syntax of lists, I chose to use square brackets [], and for dictionaries, curly brackets {}, yet again exactly like Python. This also has the benefit that valid JSON is valid Noulith².

Finally, with regard to variable scoping, Noulith has a simple approximation of lexical scoping, but names are not namespaced or qualified whatsoever. All built-ins live in the same global namespace. This is another thing that’s bad but low priority.

Operators and functions

Things should get more interesting from here. Next up: how do you perform basic arithmetic operations? I am used to adding two numbers like x + y. There are alternatives: in Lisps, for example, arithmetic operations are called prefix like (+ x y) for homoiconicity; in stack-based languages like Forth and GolfScript, they’re called postfix like x y +. Both approaches also make parsing much easier. Still, I decided either alternative would rather fundamentally slow me down as I tried to translate thoughts into code, so I stuck with the mainstream: basic arithmetic operations are infix.

Similarly, I decided that prefix unary minus was required. Which means that the - operator, if nothing else, has to be callable as either a prefix unary operator or an infix binary operator. We’ll return to this later.

Okay, what about function calls? There is again a popular syntax: foo(bar, baz). The main alternative is simply juxtaposition (and heavy currying so that this does the right thing), as in Haskell and MLs (OCaml, SML, F♯, etc.): foo bar baz. A smaller deviation is to support the popular syntax but also allow the parentheses to be omitted, as in Perl and Ruby: foo bar, baz.

Using mere juxtaposition as function invocation sort of conflicts with binary operators, which are just two arguments juxtaposed around an operator: is x + y calling addition on x and y, or calling x with arguments + and y? Most languages don’t have this problem because they have a fixed set of binary operators that are totally distinct from identifiers, but I wanted to be able to add lots of operators without enshrining them into the syntax or needing a lot of boilerplate in the implementation. Haskell and MLs resolve this conflict by parsing identifiers made from operator symbols, like +, as binary operators, while parsing identifiers made from alphanumerics, like x and y, as functions to be called with juxtaposition. So, something like a b + c d is parsed as (a(b)) + (c(d)). However, the approach I ended up liking the most is Scala’s, whose parser doesn’t draw this distinction between types of identifiers (except to determine precedence, which we’ll come back to later; and its lexer does draw this distinction, as does Noulith’s, so that x+y is three tokens while xplusy is one). Scala’s grammar just says that a b c is always a binary operator where b is called with a and c.

Well, Scala actually says that operators are methods:³ the b method of a is called with c as its sole argument. But I didn’t particularly want methods in my language, as they seemed like an unnecessary layer of abstraction for my goals. So in Noulith, b is looked up in the same scope as the identifiers around it. One can view this as combining Scala’s approach with Uniform Function Call Syntax, seen in languages like D and Nim.

Why is this approach great?

• It’s simple: after identifiers are lexed, the parser doesn’t need to know their type.
• It’s good for compositionality: it becomes easy to pass operators to other functions, like zip(+, list1, list2).
• And, well, it fits my personal taste: I like being able to use alphanumeric identifiers as infix operators, which we’ll talk about more in a bit. (You can have special syntax for doing so, like Haskell’s backticks, but I thought that was ugly for something I wanted to use extensively.)

But there’s a wrinkle we have to return to. I already mentioned I wanted to support unary minus, so -a should be the negation of a. But then how should an expression like - - a be parsed? Is it calling the middle - as a binary operator on the operands - and a flanking it, or applying unary minus twice to a? I still didn’t want to make - special in the syntax, so I decided I was okay with requiring parentheses to express the second intent, as in -(-a), and saying that (a b) is a sort of special case where juxtaposition expresses a function call, wherein a is called with one argument, b.

On the other hand, I enjoy partially applying operators a lot. They’re useful for passing into higher-order functions to produce neat expressions like (Advent of Code Day 7) some_list filter (<= 100000) then sum to sum all numbers that are at most 100000 in a list. This syntax I wanted to support is taken from Haskell, but also conflicts with unary minus. Is (-3) the number “negative 3” or the function that subtracts 3 from its input? Haskell resolves this by specifically carving out a syntactic special case for -; it is the only operator for which (-x) does not partially apply the first function in the juxtaposition.⁴ For every other Haskell operator, say +, (+x) is a partially-applied function that, given an argument a, returns a+x. I chose to emulate this behavior by still having juxtaposing two expressions mean unary function application, but then just making most built-in functions support partial application when called with one argument, but not -.

On the gripping hand, I also decided to emulate Scala here and also offer the “section” _ + x, which is also a function that, given an argument a, returns a + x. These are strictly more powerful (e.g., for reasons explained later, 0 < _ < 10 is also a valid “section” that checks whether one argument x is between 0 and 10 — unlike Scala, where this wouldn’t work because it parses as comparing the lambda 0 < _ to 10), at the cost of requiring at most two extra characters, so the argument for having these and functions rampantly supporting partial application is much weaker. Still, for now, I am keeping both syntaxes out of inertia.

On the fourth hand, Haskell also allows partially applying functions on the other side of binary operators. For example, (3-) is the function that subtracts its argument from 3. Noulith also copies this syntax by decreeing that, if a is not a function but b is, then (a b) is b partially applied with a as its first argument. This heuristic is flawed when both a and b are functions: for example, <<< is the function composition operator, so that (f <<< g)(h) is f(g(h)), but if you try to postcompose sin onto another function as (sin <<<), it won’t work. This specific case is easy to work around because you can write (>>> sin) instead, but it’s definitely a drawback.

Before we spend some time looking at the implications of making everything an infix operator, I will mention that Noulith doesn’t (currently) support named arguments. It’s one of those things that I think would be nice to have, but isn’t a priority because it matters more in longer, more structured programs, and it also comes into mild tension with a heavily functional style. One way I’d characterize the allure of named arguments is that they’d allow you to ignore, for example, which of the following two definitions a function was defined with, and use them the same way:

def foo(baz=1, quux=2): return baz - quux
def foo(quux=2, baz=1): return baz - quux

Unfortunately, the difference does matter if you want to map or zip with foo. To keep ignoring it, either you’d have to wrap foo in a lambda to plumb the right inputs to the right named arguments each time, which loses most of the elegance of functional programming, or you’d have to make all these higher-order functions take the names of arguments to use when invoking the functions you provide them, which I think is annoying to implement and to use. Still, you could imagine a language that takes that plunge. Perhaps language support at a more fundamental level would make everything work out.

Coding with and without infix functions

As I previously alluded to, I also like making everything an infix operator so I can call functions like map on a list by typing after the code for creating that list. This fits how I write code mentally: “I have this data, I will transform it in this way, then transform it in that way, then apply some final function and I’ll have my answer.” At each step I remember what form of the data is in my head and figure out what transformation I want to apply next.

To give a more concrete example, I’ll walk through 2022’s first day of Advent of Code. If I were to do it in Python, I might think to myself: okay, the puzzle input is a sequence of “paragraphs” (the name I mentally give to blocks of text separated by double newlines), so let’s break it up into such:

puzzle_input.split("\n\n")

“Now for each paragraph we want to get all ints from it…” Like many leaderboarders, I have a prewritten function ints that extracts all the integers from a string with a simple regex, but to use it I have to move my cursor to the start of the expression, type map(ints,, then move my cursor back to the end to add ).

map(ints, puzzle_input.split("\n\n"))

“Then we want to sum all the integers in each paragraph…” Back to the start of the line, map(sum,, then back to the end, ).

map(sum, map(ints, puzzle_input.split("\n\n")))

“Finally take the max…” Rinse and repeat.

max(map(sum, map(ints, puzzle_input.split("\n\n"))))

That’s six cursor jumps to write this simple four-step expression. Jumping to the start of the line is a relatively easy text editor operation, but if I were writing this expression to assign it to a variable, locating the start each time would be less fun. A language could avoid the cursor jumps back to the end of the line by making parentheses optional as in Perl or Ruby or something, but would still force me to write the ints map, the sum map, and the max call right-to-left in the order I thought of applying them. A complete solution to this issue has to make functions like map and sum callable postfix of the sequence being mapped or summed. This could be done by making them methods of lists, puzzle_input.split("\n\n").map(ints), or by providing operators like |> in F♯ and Elm. But our Scala-inspired solution not only achieves this, it dispenses with almost all the punctuation! Here’s the actual Noulith from my Day 1 solution this year, where you can see the tokens in the same order as the steps in my thought process above.

puzzle_input split "\n\n" map ints map sum then max

One downside of this syntax is that it only supports calling binary operators, i.e., combining the expression you’re building on with exactly one other argument. However, this is easily extended to support unary operations with a built-in function that just performs reverse function application, as seen above with then max. Noulith provides two such built-ins, then and . (which have different precedences): a.b and a then b are both just b(a). It’s less obvious how to chain functions that take three or more arguments, but some language decisions we’ll see in the next section actually make it pretty reasonable (not to mention that, as I observed in my previous post about code golf, functions that “naturally” take three or more arguments are surprisingly rare).

Before we move on, I want to point out that “being able to write code from left to right without backtracking” is a completely bonkers thing to optimize a programming language for. This should not be anywhere in the top hundred priorities for any “serious programming language”! Most code is read far more often than it’s written. An extra keystroke here or there is just maximally insignificant. Fortunately, Noulith is not a serious programming language, so I have no qualms about optimizing it for whatever I want.

Operator precedence and chaining

Here’s something we haven’t discussed: what is the precedence of binary operators? Is an expression like a + b * c evaluated as a + (b * c) or (a + b) * c, and why?

There are quite a few options. Most languages just determine this with a big table, e.g., here’s C++’s operator precedence, but this won’t work for a language like Noulith that supports using arbitrary identifiers as operators. In OCaml and Scala, precedence is based on a similar table that classifies all identifiers by their first character: so, for example, every operator whose name begins with * binds more tightly than every operator whose name begins with +. You can also make this more customizable: in Haskell, you can declare the precedence of operators as you define them with fixity declarations, while in Swift (via, via), you can declare “precedence groups” and assign infix operators to them, and each group can state whether it binds more or less tightly than other groups. While these approaches are neat, they complicate the parsing story quite a bit. You need to parse earlier code to the extent that you know each operator’s precedence before you can parse later code correctly, whereas I wanted to implement a simple parser that didn’t have to think about global state. Finally, some languages like Smalltalk and APL (and APL descendants) dispense with precedence entirely: all binary operators are left-to-right in Smalltalk and right-to-left in APL, which means you can’t rely on the precedence for arithmetic operators and equality you learned in math class. I think getting used to it isn’t too bad, but decided it was still worth trying to avoid.

Alongside this question, though, I was considering an even more difficult goal: I wanted to be able to chain comparisons like in Python, e.g., 0 <= x < n. This kind of testing if something is in range is common, and having to write expressions like 0 <= x && x < n annoys me, especially when x is a complicated expression I don’t want to write twice or stick in an intermediate variable. It’s also an extra opportunity to make a mistake like 0 <= x && y < n — I’ve written these bugs and struggled to find them before. So, how might I add this syntax feature?

Syntax support for chained comparisons is rare among programming languages because it’s “pure syntax sugar” that doesn’t let you write more interesting code (despite my complaints, stashing the middle expression in a variable isn’t a big deal) and is just generally unpleasant to parse. After Python, I think the most well-known languages to support chained comparisons are Raku and CoffeeScript. I also learned that there is a C++ proposal to add them, though it doesn’t seem likely to get anywhere. I worked briefly with a Mavo implementation that bolted comparisons on top of a parse tree from a library. But all of these languages achieve this goal by privileging comparison operators in the syntax, whereas I wanted them to be parsed the same way as every other symbolic identifier.

While researching this further, I found a particularly neat method of support in Icon (via), where comparison operators are left-associative in the normal way, but “just work” as follows (based on my understanding after reading the Icon documentation for two minutes):

• Expressions either “succeed and produce a result” or “fail”.
• If a comparison is true, it succeeds with its right-hand-side as its result. Otherwise, it fails.
• Control flow statements check whether an expression succeeds rather than what its result is.

So in Icon, a chained comparison a < b < c is evaluated by first evaluating the subexpression a < b; if a is less than b, this simplifies to b and then checking if b < c; if either comparison isn’t true, the expression fails. If both comparisons pass, the expression evaluates to c, but that doesn’t matter, because the only important criterion is whether the expression succeeded. While this is cute, I didn’t want to overhaul what “evaluating an expression” means in Noulith to include an additional success/failure status, just to allow chaining comparisons. Not to mention, I enjoy having the option to treat the truth value of a comparison as an integer, e.g., to index into an array or sum in a loop. I’m not aware of any other programming languages that support chained comparisons without privileging them in the syntax (except perhaps in some really abstract sense where code can change how subsequent code is parsed, like in Coq or something).

Fundamentally, I wanted a parsing strategy that could handle expressions like @ = <=; @@ = <; a @ b @@ c. If I parse a @ b @@ c as a tree of binary operator invocations, with either nested under the other, I’ve already lost. There’s no way to recover what was really intended. Consider, for example:

switch (random_range(0, 3))
case 0 -> (@, @@ = <=, <)
case 1 -> (@, @@ = +, *)
case 2 -> (@, @@ = *, +);
print(1 @ 2 @@ 3);

There’s simply no way to know which of @ and @@ binds more tightly until the random number has been generated, long after the code’s been parsed. So I concluded that Noulith had to parse a @ b @@ c as a flat list of three operands and two operators, and deal with precedence at runtime. In brief, what happens then: every operator function is examined at runtime to resolve whether it “chains” with the next operator to produce a single operator invocation subexpression, and then to resolve which operators bind the most tightly.

From there, it was easy and natural to make operator precedence accessible and mutable by users. Without thinking too hard, I threw it under a string key "precedence" just to get something working, so I could take a cool screenshot and post it on Twitter. Then it stayed there out of inertia. Here’s a remake of that screenshot with the newest syntax and highlighting.

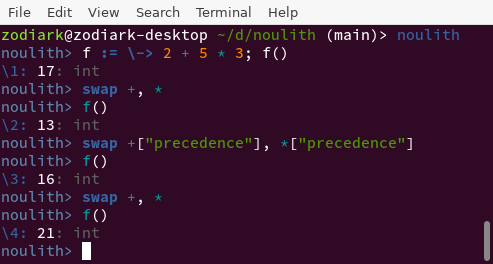
While this is probably deeply disturbing to any parser enthusiasts out there, it opens up the field for us to easily add chaining support to basically any operator, and there are actually some additional “nice” side effects of this!

• Cartesian product and zip operators can behave more nicely with three or more operands. If zip were a normal left-associative binary operator, then the result of [1, 2, 3] zip [4, 5, 6] zip [7, 8, 9] would begin with [[1, 4], 7]. But by allowing zip to recognize when you’re immediately zipping its output with another sequence, you can produce a result that starts with [1, 4, 7]. The only other language I’ve seen that supports something like this is TLA⁺’s Cartesian product ×,⁵ though I have no clue how to search for this kind of syntax in other programming languages.

• Runs of binary operator invocations can naturally include functions that take more than two arguments. By saying that replace chains with with, I allow you to tack replace b with c onto the end of a sequence of binary operators.

• Finally, functions can have “optional arguments” while still being called in the same binary operator style. By saying that to and til chain with by, I allow the expression 1 to 10 by 2 without affecting the meaning of 1 to 10. (Scala achieves the same effect without parsing shenanigans by having ranges being aware of what kind of range they are and supporting by as a method.)

Another implementation detail of note is that Noulith precedences are floating point numbers. I thought this was natural because it seems that every programming language with only a few precedences, like Haskell’s 10, eventually gets complaints that there’s no room to fit an operator’s precedence between two existing ones. Some languages hedge by leaving gaps, the way BASIC programmers spread out their line numbers in the 1970s (or so I’m told) and CSS developers spread out their z-index values, just in case you need to insert something in-between later: Coq uses precedences from 0 to 100, with defaults mostly at multiples of 5 or 10; Prolog, from 0 to 1200 in multiples of 50 or 100; Z, at multiples of… 111? But floating-point precedences let you leave finer gaps with less foresight. I imagine other languages don’t do the same for reasons along the lines of, the semantics of floating-point numbers are too complicated and unportable for a core feature of language syntax to depend on them. (What if an operator’s precedence is NaN?) I can sympathize a lot with this, but as I have no ambitions for Noulith to become a language with a formal specification, I didn’t mind.

Finally, I should mention the standard boolean “operators” and and or. These operators are, and have to be, special in most programming languages because they need to short-circuit — in an expression like a and b, if a evaluates to something falsy, then b is not evaluated, which is important for both efficiency and correctness. For example, you can check if an index is in bounds for an array on the left side of an and and then perform the actual indexing on the right; without short-circuiting, the indexing would still be attempted when the index is out of bounds, causing an error. and and or can be normal functions/operators in some languages with easily accessible lazy evaluation like Haskell, or normal macro constructs in other languages like Lisps. Unfortunately, Noulith lacks both faculties, so its and and or do have to be language constructs. As in Python, these expressions return the last or first truthy expression they encounter (e.g., 2 and 3 is 3 instead of just “true”), enabling them to emulate conditional expressions in some contexts. I also added the SQL-inspired coalesce, which is similar to or but only rejects null as its left operand, with the vague idea that it could be used in more precise “default value” setups, but barely ended up using it. (However, not does not need any special behavior, so it’s just a normal function.)

Variables, statements, and blocks of code

We’re finally graduating from expressions to statements. First up: How do you declare a variable? I was just going to copy Python at first and use a simple = for both declaration and assignment, but then I read the Crafting Interpreters design note on implicit variable declaration and was utterly convinced, so I started looking for a syntax to distinguish them.

In some statically typed languages (mostly C/C++/C♯ and Java), variable declarations start with the variable’s type merely juxtaposed with its name. I’m not sufficiently invested in static types to want this, but even if I were, since I already decided that juxtaposition can be function invocation, trying to copy this exact syntax basically means that Noulith has to immediately be able to tell whether it’s parsing a type or an expression when starting to parse a statement. This is doable by a strategy like saying that types have to be capitalized or something, but… it’s complicated.

Still, there are many other viable choices. let? var? my? Heck, I could spell out variable as in Ceylon. In the end I landed on using :=, sort of like Go or even Pascal, both for succinctness and because I realized I liked the option of being able to declare types sometimes (like Python 3 annotations, as used by type checkers like mypy): conveniently, a declaration like a := 3 can be seen as a special case of a declaration like a: int = 3 where the type is omitted, which Noulith also supports. Of note is that Noulith checks the values assigned to typed variables at runtime, so the following errors:

a: int = "hi"

As does this:

a: int = 6;
a = "hi"

This is bizarre and silly — usually you don’t want type annotations to have any runtime cost, much less every time you assign to an annotated variable — but it catches some bugs and is way easier to implement than a static analysis pass, plus it’s consistent with a more reasonable behavior for typed patterns in pattern matching, which we’ll talk about much, much later.

Another advantage is that by thinking of x: as a general lvalue (crudely, a “thing that can be assigned to”), this syntax naturally generalizes to single assignments that simultaneously assign to an existing variable and declare a new one: x := [3, 4]; (a:), b = x. (Go’s short variable declarations are somewhat magic here: you can use a single := to simultaneously declare some new variables and assign to some old ones, as long as at least one variable is new. I think this is slightly inelegant, and sometimes daydream about Evan Miller’s proposal whereby you need to write exactly as many colons as variables you’re newly declaring. But as my gripes with languages go, it ranks pretty low.)

Also unlike Crafting Interpreters, I don’t allow redeclaring a variable with the same name in the same scope. The book makes a really good point that this is annoying for REPL usage, where programmers might just want to use and reuse variable names without mentally tracking which ones have been declared so far. I have not made up my mind here yet, so redeclarations are banned for now, mostly because it’s easier to make rules laxer than stricter as the language develops, but I suspect I’ll end up lifting this restriction at some point.

Next: how are statements and blocks of code (for control flow branches, e.g.) delimited? I used to like indentation-based structure a la Python, the idea being that, because you want your code to be indented to reflect its structure for the human reader anyway, having your language also require braces or other delimiters is redundant. However, I’ve learned to appreciate that redundancy is not inherently bad, and control flow that’s delimited with only indentation is actually quite annoying to refactor. When you have a block of nested code that you want to move around, you have to track its indentation much more carefully than you’d need to if there were explicit delimiters. For example, suppose I wanted to inline the call to f in this Python code:

def f(x, y, z):
    # blah blah blah
    print(x + y + z)
for x in xs:
    for y in ys:
        for z in zs:
            # other stuff
            f(x, y, z)
        # other stuff

I might try copying the body of f where I want it to go, replacing the call to it, which seems like it should work because its arguments and parameters are exactly the same. Uh-oh:

for x in xs:
    for y in ys:
        for z in zs:
            # other stuff
    # blah blah blah
    print(x + y + z)
        # other stuff hanging out here

This code is currently broken, and to fix it I have to indent the two lines I copied exactly twice, while taking care not to indent the lines next to it. This is an exaggeratedly simple case, but the block of code being transferred might have its own internal indentation or other internal details that must be kept track of, like parameter names that need to be changed, making the transfer much trickier. On the other hand, in a similar language with braces, the copy-pasted code would be syntactically and semantically correct with no extra effort, and its indentation can trivially be fixed by any competent text editor.

for x in xs {
    for y in ys {
        for z in ys {
            # other stuff
    # blah blah blah
    print(x + y + z)
        }
        # other stuff hanging out here
    }
}

To defend the indentation solution, I might say that this is rare and that the right way to avoid it is to avoid deeply nested code in the first place, or just to get better editor support (I haven’t spent enough time in large Python projects to look into more sophisticated tooling, but I assume it exists). I’d also point out all the other costs of the braces-based solution, such as the blank lines with only }s in them. I don’t think this is a terrible defense — deeply nested code is often worth avoiding. But I wanted Noulith to support code without a lot of effort put into structuring it and breaking things into functions, so I chose to stick with explicit delimiters.

What delimiters, though? Unusually, I ended up using more parentheses, rather than the far more common curly braces, because I found the simplicity of not distinguishing expressions and statements quite appealing. Scala (at least, version 2) is one language where some blocks can be written with either parentheses or curly braces, which are similar but have subtly different semantics, and I didn’t want to think about that. This led me to follow C/C++/Rust and always require statements to be separated by semicolons, because if any expression can be a series of statements, and if a language’s syntax is so flexible in other ways, it’s really hard to guess when a newline is meant to end a statement. Other languages can say that line breaks don’t count inside parentheses, or have even more complicated rules for automatic semicolon insertion; but the flexibility of Noulith syntax means code like the contents of the parentheses below really could make sense as one large expression or as two expressions (the latter of which calls * with one argument to partially apply it).

x := (2
# hello
* 3)

All this does make Noulith’s parser incredibly bad at recovering from mistakenly omitted semicolons, which is one reason I’d wholeheartedly disrecommend anybody try to write Noulith programs that are larger than quick-and-dirty scripts. It’s probably too late to fix this at this point, and in hindsight, perhaps I should have thought a bit more about alternatives before allocating both square and curly brackets to literals. Still, I don’t know if I would have decided any differently. I like all the other features I got for this tradeoff.

Control flow

Having discussed most of the decisions surrounding simple expressions and statements, we can turn our attention to control flow structures.

A fundamental syntactic issue most languages have to grapple with: in the syntax for a construct like if condition body or while condition body, you need some way to decide where condition stops and body starts. There are a couple options:

• You could use a keyword like if condition then body (e.g. Haskell, Ruby) or while condition do body (e.g. various POSIX shells, Scala 3).
• You could use punctuation like if condition: body (e.g. Python).
• You could require parentheses (or some other delimiter) around the condition like if (condition) body (e.g. C/C++, Java, JavaScript).
• You could require braces (or some other delimiter) around the body like if condition { body } (e.g. Go, Rust). (Note that this only works if legitimate conditions never contain the delimiter,⁶ so doing this with parentheses wouldn’t work in Noulith and most other languages.)

I partly locked myself out of considering the last option by allocating curly brackets to sets, but I think that for my use case, I still preferred the old-school C-like solution of parenthesizing the condition because I often wrote nested control structures with bodies that were long but only comprised a single expression. In such cases, I thought it was less mental load to type the closing parentheses sooner. For example, I thought this:

if (a) for (b <- c) if (d) e;

looked neater and easier to write than this:

if a { for b in c { if d { e }}};

I also copied from Scala/Rust the ability to use if/else constructs as expressions, which just return whatever the last expression of the taken branch evaluate to, so you can write code like:

print(if (a < b) "a is less" else "b is less or equal")

Semantically, this construct (and all others that care about “truth value”, e.g., filter predicates) determine truthiness just like Python, where 0 (which false is a synonym for), null, and empty collections (lists, strings, dictionaries, etc.) are falsy and all other values are truthy. This is another choice I made without much thought, and is not at all the only plausible one — you could, for example, consider 0 truthy like Ruby and most Lisps, or consider empty lists truthy like JavaScript. You could consider the string "0" falsy like PHP and Perl. You could consider everything other than true false like Dart. If you want to be really adventurous, you could consider integers truthy iff positive, like Nibbles; or iff equal to 1, like 05AB1E; or if they’re ≥ 0.5, like in Game Maker Language (in some contexts?) The Pythonic rule makes sense to me in that it does something useful for most data types, but I suspect that this is mostly just because I’m used to it.

On ternary expressions

I have to go on another mini-rant here. Ternary expressions are an important feature of programming languages to me, and I am still annoyed that Go doesn’t have them. Critics say they’re confusing and can always be replaced by if-then-else statements — code like:

var foo = bar ? baz : quux

can always be rewritten as:

var foo
if (bar) {
    foo = baz
} else {
    foo = quux
}

This is six lines instead of one. Now, I try not to let my code golf tendencies seep into other contexts, but even so I think six lines instead of one is an unacceptable amount of verbosity and actually makes the code much harder to read, particularly in cases when all the constituent expressions are really that short. The distance between foo’s declaration and initialization also means that readers have to deal with the mental load of worrying “is foo going to be initialized?” when reading this code.

One might propose the shorter four-line alternative in response, which often works:

var foo = quux
if (bar) {
    foo = baz
}

Even ignoring the cases where evaluating quux has side effects that break this rewrite, what I don’t like about this code is that to readers, the first statement var foo = quux is a lie. Semantically, it appears that the code is stating an unconditional fact that foo should be defined as, or at least initialized to, quux; so if quux is a complicated expression, readers might be mulling over how to understand that fact. For an example (taken directly from Noulith itself), say I was implementing an interpreter that took one command-line argument, which could be either a filename or a literal snippet of code, depending on a flag. The single-branch if might look something like:

var code = arg
if (flag) {
    code = open(arg).read()
}
// lex, parse, and execude code...

arg is sometimes a filename, in which case it is definitely not a snippet of code. If a reader already know this, or perhaps guessed it and is skimming the code to verify whether it’s true, and they read the line var code = arg, they’ll stumble. Of course, they’ll probably figure out what’s going on if they keep reading two more lines, but why permit this confusion to occur in the first place?

I can, however, sympathize with believing that ? : is too cryptic, so I most prefer Rust and Scala’s approach of just accepting the entire if/else construct to be an expression, allowing code like:

code := if (flag) {
    open(arg).read()
} else {
    arg
}

This is honest and avoids ever suggesting to readers that code is unconditionally something it’s not. It’s also easier to fit on one line (though linters might complain).

Loops

With if/else out of the way, we can move on to loops. Noulith has while loops, which are quite unremarkable, but no do ... while loops or infinite loops yet. The for loops (which are all “for-each” loops) are more interesting, though, and are one of the few features that I added under one syntax, worked with and wrote code using for a long time, and then went back to change the syntax of. Specifically, I started with the C++/Java-style for (a : b), plus the quirky generalization for (a :: b) for iterating over index-value or key-value pairs. But eventually I concluded this interfered too much with wanting to use : for “type annotations”, so I swapped out the separator after the iteration variable to be <-, as in Haskell and Scala. (in as in Python and Rust was not a serious contender because I preferred to allocate that to be used nonsyntactically as a function; design choices thus far prevent it from doing double duty. I didn’t want something :=-based as in Go just because the symbol := does not suggest that to me.) I also copied Scala to provide a feature I use a lot in search-type scripts, allowing multiple iterations in a single loop, as well as if guards.

for (a <- as; b <- bs; c <- cs; d <- ds; if cond(a, b, c, d)) e

Also from Scala I copied the ability to modify this into a list comprehension:

for (a <- as; b <- bs; c <- cs; d <- ds; if cond(a, b, c, d))
  yield e

Finally, inspired by several Discord conversations, I also allow dictionary comprehensions:

for (a <- as; b <- bs; c <- cs; d <- ds; if cond(a, b, c, d))
  yield k: v

I don’t have much more to say about these loops, except perhaps to note that they really are just for iteration, instead of being syntax sugar for monads or anything like that.

Structs

This is a short section because this was a last-minute addition and I haven’t really used it much yet, but Noulith supports structs, which are super bare-bones product types.

struct Foo(bar, baz);

Each instance of Foo has two fields. The variables bar and baz are “reified fields” that can be used as member access functions, and also used to assign or modify the fields with the same indexing syntax as everything else.

foo := Foo(2, 3);
bar(foo); # evaluates to 2
foo.bar; # just function application, evaluates to 2 for the same reason
foo[bar] = 4;
foo[bar] += 5;

The most notable aspect is that bar and baz are actually just newly defined variables holding these field objects, and not namespaced under the struct Foo in any way. Noulith will not let you define another struct with a field named bar or baz (or any other variable with either name) in the same scope. This was basically the lowest-effort way I could think of to get usable structs into the language, and the only thing I’ll say in defense of this design is that Haskell record fields have hogged their names in much the same way until maybe 2016, when GHC 8 released DuplicateRecordFields, and is still experimenting with language extensions like OverloadedRecordUpdate. So I’m allowing myself at least two decades to figure out something better.

Pattern matching, lvalues, and packing/unpacking

Noulith has switch/case for basic pattern matching. (Example lifted from Python’s pattern matching tutorial.)

switch (status)
case 400 -> "Bad request"
case 404 -> "Not found"
case 418 -> "I'm a teapot"
case _ -> "Something's wrong with the Internet"

(A syntactic observation: because we have the case keyword and because switches don’t make sense without at least one case, the parentheses around the switch argument aren’t necessary like they are with if or while. Noulith’s parser still requires them for now for consistency, but perhaps I should lift this requirement…)

Unlike some similar constructs in other dynamic languages, Noulith’s switch expressions error out if no cases match, even though there’s a solid case to be made for doing nothing and returning null. This is a change I made during Advent of Code after writing too many bugs caused by mistakenly omitted default cases.

Other than check for equality with constants, pattern matching can destructure/unpack sequences:

switch (x)
case a, -> "one"
case a, b -> "two"
case a, b, c -> "three"
case a, b, c, ...d -> "more"

One gotcha, shared with many other languages’ pattern-matching, is that variable names in patterns always bind new variables, whereas sometimes you want to check equality against a previously defined variable. This code, for example, will not do what you want. The pattern will always match and define a new variable named not_found equal to x.

not_found := 404;
switch (x)
case not_found -> "Not found"  # pattern will always match

Scala and Rust both allow you to work around this by supporting constants that are syntactically distinct from variables; Python supports “constant value patterns” that must be dotted, which I think is fortunately common. Noulith’s slightly more general workaround is the keyword literally, which turns an expression into a pattern that evaluates the expression and checks for equality.

not_found := 404;
switch (x)
case literally not_found -> "Not found"

Patterns can also check the type of values at runtime (which is why this check also occurs when declaring variables):

switch (x)
case _: int -> "it's an int"
case _: float -> "it's a float"

To implement the analogue of many languages’ even more general patterns, “pattern guards”, that let you check for arbitrary predicates, you can manufacture arbitrary types with satisfying (which is a normal function). I am not sure this is “right”, but it was easy.

switch (x)
case _: satisfying(1 < _ < 9) -> "it's between 1 and 9"

Notably missing is the ability to destructure custom structs, partly because I haven’t gotten around to it and partly because there are concerns about how this interacts with augmented assignment, which we’ll talk about much later.

In hindsight, I don’t know why I used the extremely old-school C/C++/Java switch keyword. match makes much more sense and is popular today. Even Python adopted it. But it is what it is for now.

Anyway, my experience was that you don’t need a lot of capabilities for pattern matching to be really useful. The trivial product type provided by sequences is enough to approximate sum types just by manually tagging things with constants. Also, pattern matching is just really useful for parsing Advent of Code strings. Day 7 (my full code) might be the best example:

switch (line.words)
case "$", "cd", "/" -> (pwd = [])
case "$", "cd", ".." -> pop pwd
case "$", "cd", x -> (pwd append= x)
case "$", "ls" -> null
case "dir", _ -> null
case size, _name -> (
    for (p <- prefixes(pwd)) csize[p] += int(size)
)

In languages without pattern matching, the simplest way to handle this might be to write a bunch of deeply nested if/else statements that look like the following, which is a pain to read, write, and debug:

if (a == "$") (
    if (b == "cd") (
        if (c == "/") ( ... )
        else if (c == "..") ( ... )
        else ( ... )
    ) else if (b == "ls") ( ... )
)

It happens that Day 7 is the only day on which I was first to solve either Advent of Code part, and I got first on both that day. Perhaps this was a factor?

However, Noulith’s pattern matching has its own issues. Here is a pattern that’s surprisingly tricky to support, which I only realized in mid-September:

switch (x)
case -1 -> "it's negative one"

Obviously, we want the case to match if x equals -1. The analogous pattern for nonnegative integers works with the simple, obvious rule: a value matches a literal if they’re equal. Unfortunately, -1 is not a literal — it’s a function invocation! Outside a pattern, it calls unary minus on the argument 1.

The simplest way to resolve this is to say that, when parsing a pattern, - gets attached to the subsequent numeric literal if one exists. Python’s pattern matching, for example, specifically allows - in the syntax for literal patterns — as does Rust, as does Haskell. As for Scala, its literal patterns are syntactically the same as its literals, which encompass a negative sign in every context. One reason this makes sense for it but not the other languages I just listed is that, courtesy of its Java/JVM lineage, the sets of legal positive and negative integer literal are not symmetric because they represent two’s-complement machine words. Specifically, -2147483648 is a legal Java/Scala expression, but 2147483648 by itself is a compile-time error. (Therefore, so is -(2147483648)! I first learned this from Java Puzzlers.)

But returning to Noulith: having gotten this far without privileging - in the syntax, I decided to try a little harder. Thus, I had pattern matching “ask” the function - how to destructure the scrutinee into an inner pattern. That is, to see whether x matches the pattern -1, Noulith resolves the identifier -, determines that it means negation in a pattern-matching context, negates x, and matches that against the pattern 1.

This means that pattern matching like this works as well:

switch (x)
case -y -> print(x, "is negative", y)

This makes it easy to support a bunch of other, somewhat ad hoc patterns, like allowing fractions to be destructured into their numerator and denominator.

switch (f)
case x/y -> print("numerator is", x, "and denominator is", y)

Or checking for divisibility. Because we can.

switch (x)
case 2*k -> print(k, "pairs")
case 2*k + 1 -> print(k, "pairs with one left over")

But the most “evil” pattern-matching mode I’ve implemented is probably for the comparison operators. A pattern like 1 < y < 9 matches any number that is greater than 1 and less than 9, and binds that number to y. More generally, a chain of comparison operators with one variable matches any value that would satisfy those comparisons. But if the chain has X variables where X > 1, it matches any list of X values that would satisfy those comparisons if plugged in.

xs := [2, 7];
switch (xs)
case 1 < a < b < 9 ->
  "two strictly increasing numbers between 1 and 9"

This works because, before an expression is matched against a pattern, there’s a preparatory pass through the pattern that evaluates literals and literally expressions and presents them to the function, so that any function asked to destructure something during the matching process knows which of its operands are known values and which are other patterns that it might send something downwards into. Also, functions determine their precedence and chaining properties as they would outside a pattern. So, the three <’s in the above example chain into one function that is then asked whether it matches [2, 7], with the information that it has four “slots”, the first and fourth of which contain values 1 and 9 and the second and third of which are its responsibility to fill. However, it does not know any more specifics about what patterns produced those values or what patterns are in the slots it has to fill. Its view of the situation is the same as in the following example (which also succeeds… at least after I fixed a bug I found while writing this post):

xs := [2, 7];
switch (xs)
case 1 < 2*a < 2*b + 1 < literally 3*3 ->
  "an even number and then an odd number, both between 1 and 9"

I had to look all this up in the code to remember how it works. I think I wrote this while possessed by the dragon. Still, being able to write notation like this pleases my inner mathematician.

The last feature of patterns is or, which can be used to combine patterns to produce a pattern that matches if either subpattern matches. I think | is a lot more popular in other languages, but again, I wanted | to be a normal identifier in the syntax. Pattern-combining has short-circuiting behavior that can’t be implemented by a normal pattern-matching function, just like or in an expression can’t be replaced by a function, so it made sense to me.

The other control flow structure using pattern matching is try/catch.

try 1//0
catch x -> print(x)

The code in the body of the try is evaluated normally, except that if an exception is thrown, the exception is checked against the catch clause’s pattern in much the same way a case clause checks whether the switch argument matches a pattern; if it matches, the catch’s body is evaluated and the exception is not propagated further. For whatever reason, I only allow each try to accept one catch clause now, even though it would be easy and more sensible for each try to accept multiple clauses, the same way one switch accepts multiple cases. I have no excuse except laziness. Maybe I’ll implement it after finishing this post.

As previously mentioned, Noulith doesn’t have a special type for exceptions or errors, even though it “should”. You can just throw and catch any value you can store in a variable. Most (all?) errors thrown by built-in functions are just strings for now, and most of my Advent of Code solutions just throw and catch the string "done". The extraordinarily poor error handling is another reason nobody should write production code in Noulith.

Pattern matching is also useful in mere assignments, for destructuring a sequence and assigning different parts to different variables…

foo := [1, 2];
a, b := foo

…as well as in functions’ parameter lists. So let’s turn to those next.

Functions

What do functions and lambdas look like?

I love lambdas and want Noulith to support functional programming extensively, so a keyword like Python’s lambda is definitely too verbose for me. This isn’t a syntax where there’s much uniformity across programming languages to be found, so I went with Haskell’s short, snappy \, which I think is supposed to look like an actual lambda λ if you squint. (The really “fun” option would have been to directly use U+03BB λ, which is actually easy for me to type with a Vim digraph, Ctrl-KL*; but I’m not that adventurous and didn’t think I’d do anything else with \ anyway. Not to mention, λ is a Letter, the wrong Unicode General Category.) The rest of the syntax is a mix of Python and Haskell: parameters are delimited with commas, but the parameter list is separated from the body with ->.

\a, b -> a + b

On reflection, I realized many programming languages don’t start lambdas with a prefix sigil at all, e.g., JavaScript and Scala have arrow functions similar to x => x + 1 or (x, y) => x + 4; you just parse a comma-separated list of expressions, then when you see an arrow you turn that expression into an argument list. This doesn’t make parsing meaningfully harder because I already have to do similar backtracking when parsing the LHS of an assignment. But using a prefix sigil does allow me to continue to reject () as a syntactically invalid expression, instead of accepting it in some contexts to express a lambda with zero parameters () => x. Plus, a prefix-less syntax would make parse errors even more fragile. So I was satisfied sticking with \.

Finally, I decided I was comfortable enough with lambdas that I didn’t feel the need to design and add a separate syntax for declaring named functions. Just make a lambda and assign it to a variable. One drawback, though, is that it’s sometimes useful for debugging or metaprogramming for functions to know what their own names are, so I wouldn’t rule out adding a syntax for defining and naming a function one day.

While we’re talking about lambdas, let’s talk about a common lambda-related pitfall and one of Noulith’s weirdest keywords. Quick, what’s wrong with the following Python code?

adders = [lambda x: x + i for i in range(10)]

The problem, which many a Python programmer has been bitten by, is that all the lambdas close over the same variable i, which is shared between loop iterations. When the loop concludes, i is 9, so all of the functions add 9. Even worse, if you were building adders in an imperative for loop, you could still mutate i outside the loop (for example, by accidentally using it in another loop).

for i in range(10):
    adders.append(lambda x: x + i)
i = 1000

This issue is less likely to appear in Noulith. Firstly, partial application is way more common, often obviating explicit lambdas, and the act of partial application grabs the variable’s value rather than closing over it. Secondly, Noulith for loops get a fresh iterator variable in each loop iteration, so even if you did make explicit lambdas like the above, they’d close over different variables — one of very few breaking changes (possibly the only one?) being considered for Go 2, which should attest to how treacherous the alternative is. The associated discussion has fun tidbits like:

Loop variables being per-loop instead of per-iteration is the only design decision I know of in Go that makes programs incorrect more often than it makes them correct.

We built a toolchain with the change and tested a subset of Google’s Go tests […] The rate of new test failures was approximately 1 in 2,000, but nearly all were previously undiagnosed actual bugs. The rate of spurious test failures (correct code actually broken by the change) was 1 in 50,000.

Still, if you wanted to artificially induce this mistake, you could write something like:

i := 0;
adders := for (_ <- 1 to 10) yield (
    i += 1;
    \x -> x + i
)

Pretend that you can’t use a unique loop variable or partial application due to other complications in the code. How could you make the code work as intended anyway?

One approach, common in older JavaScript, would be to use an immediately invoked function expression (IIFE). Translated to Noulith, this would be:

i := 0;
adders := for (_ <- 1 to 10) yield (
    i += 1;
    (\i -> \x -> x + i)(i)
)

Noulith doesn’t have this feature (yet), but another approach you can often get by with in Python is using a default argument (though this risks swallowing later mistakes where adders’s elements are called with two arguments, and might not work if you wanted to do deeper metaprogramming on the functions):

for i in range(10):
    adders.append(lambda x, i=i: x + i)

But I don’t find either of those totally satisfying. Noulith offers a different way out with the freeze keyword:

i := 0;
adders := for (_ <- 1 to 10) yield (
    i += 1;
    freeze \x -> x + i
)

freeze takes an arbitrary expression, usually a lambda, and eagerly resolves every free variable to the value that that variable holds. So in the lambda produced by freeze \x -> x + i, i is “frozen” to the value the variable i held at the time of production (and so is the operator +). Aside from the semantic change, freeze can also be used as a mild optimization, since otherwise the lambda would have to look up i and + by their string names in the environment on each invocation (something that could be optimized out by more intelligent compilers, but: effort!)

On reflection, this took a stupid amount of work for what amounts to a party trick, but I was able to reuse some of the work for static passes later, so it worked out.

Augmented assignment

In addition to the unpacking/pattern matching we’ve already discussed, many programming languages also support another variant of assignment statement sometimes called augmented assignment, as in x += y. This is often described as simply being shorthand for x = x + y, but many languages actually have surprising subtle semantic differences between the two. In C++, I believe they are the same for numeric types, but classes can overload individual augmented assignment operators like += separately from each operator +. In Python, if x is a mutable list, x += y will mutate x but x = x + y will make a new copy, which matters if some variable elsewhere holds reference to the same list. Even in that bastion of unadventurous languages, Java, x += y and x = x + y have subtle differences involving type coercion and sometimes when one of the arguments is a String (see Java Puzzlers 9 and 10). Noulith has its own subtle semantic difference, but let’s talk about the syntax first.

I definitely wanted to support +=, but unlike most languages with such operators, + is just an identifier, and I didn’t want to go through every operator and define an augmented variant. So I thought it made sense to allow any function f to be part of an augmented assignment f=, regardless of whether f’s name is alphanumeric or symbolic. This feature got Noulith a shoutout in Computer Things.

I do think this syntax feature is practical. I have often wanted to write assignments like a max= b or a min= b in search problems, where a is a variable tracking the best score you’ve achieved so far and b is a score you just achieved. These constructs are so useful that I include them in my competitive programming template as minify and maxify, with definitions like the following, and I’ve found at least a few other templates online with similar functions. (I won’t link to any concrete examples because most of the results look like SEO spam, but I am confident many competitive programmers other than myself do this.)

template <class T> void minify(T & a, const T & b) { if (a > b) a = b; }
template <class T> void maxify(T & a, const T & b) { if (a < b) a = b; }

Not only that (and I totally forgot about this until writing this post), a silly “competitive programming preprocessor” I briefly tried to create in 2015⁷ borrowed the operator spellings <? and >? of min and max, respectively, from LiveScript so that they could be used in augmented assignment. So this has been something I’ve wanted for a long time. More prosaically, though, the augmented assignment with an alphanumeric identifier that I’ve used by far the most often is append=. All in all, I wanted to support augmented assignment for any identifier, alphanumeric or symbolic.

There are several difficulties, though. Most immediately, the overwhelmingly common comparison operators conflict with making this syntax fully general, or even merely applicable to all symbolic identifiers: x <= y is definitely not the augmented assignment x = x < y. This was one place where internal and external consistency came into hard conflict and I couldn’t see how to get everything I wanted without some syntax special casing. So, Noulith’s lexer specifically treats the four tokens ==, !=, <=, and >= specially. All operators whose names end with = are lexed as meaning augmented assignment, except for those four. In hindsight, I could have looked harder for precedent: Scala has very similar carveouts, but additionally carves out any symbol starting and ending with =.

Even with that decided, it’s not clear how exactly in which stage of lexing and parsing this should be handled. Right now, the lexer parses tokens like += as two separate tokens, so the parser just parses a += 3 as assigning 3 to a +. This way, augmented assignments look the same to the parser no matter whether the augmenting operator’s identifier is alphanumeric or symbolic. Then, the left-hand side a + is parsed as a call expression, the same kind used in juxtaposition for unary operators; and when a call expression is assigned to, it performs an augmented assignment.

This works, but is actually a huge problem for internal consistency. Did you notice it? We already decided that in pattern matching, a pattern like a b, which is a function call, is a “destructure” with a: we give a the value we’re matching the pattern against, and it tells us what value we should match against b. This allows us to effectively pattern-match against negative numbers by having a be - and b be a numeric literal. But this conflicts with wanting it to mean to augment the assignment with b as the function when on the left of an =. Alas, these two interpretations just coexist in an uneasy tension for now; assignments check for the augmented assignment interpretation before allowing any destructuring, but that check is omitted in other pattern matching contexts.

This might seem like a reasonable compromise at first: augmentation doesn’t make much sense when pattern matching in a switch/case or try/catch, which should always bind new variables; and destructuring often doesn’t make sense with a single argument on the left-hand side of an assignment, which should be irrefutable. -x := y is horrible when x := -y works. But I don’t have a satisfying way to reconcile this with a syntax for destructuring structs I’d like some day. Ideally, given a custom product type like struct Foo(bar, baz), both pattern-matching and simple assignment destructuring would work:

switch (foo) case Foo(bar, baz) -> print(bar, baz);

Foo(bar, baz) = foo

But then the second assignment looks like it has a call on its left-hand side, which we currently parse as augmented assignment. One idea would be to only interpret LHS calls as augmented assignment when the call has one argument, but that seems inelegant and I think custom structs with one field should be well-supported, since they’re useful for emulating sum types. Another idea would be to distinguish a b and a(b) in LHSes, interpreting the parentheses-free version as augmented assignment and the parenthesized version as destructuring. However, augmented assignment with a parenthesized operator, such as (zip +), isn’t that outlandish (though I might well conclude that forgoing this ability is the least bad option):

a := [2, 5, 3];
a (zip +)= [4, 9, 2];
a # [6, 14, 5]

Perhaps the interpretation should be chosen at runtime based on whether the participating identifiers/expressions are defined or what they evaluate to, like how juxtaposition decides to partially apply the right function on the left argument? This seems… very messy.

Perhaps the lexer should take on more responsibility, lexing code like += and f= as single tokens that “mean” + or f with an = attached, so that a b = is a destructure but a b= is an augmented assignment? But we also wouldn’t want the lexer to consider the first token of x==y to be x=… right? Or perhaps we could, and require programmers to include the space between x and == when writing an expression like x == y? Or perhaps the lexer can get just one extra character of lookahead? This is all to say, this is one of the corners of the language design I’m the most uncertain about.

Anyway, onto Noulith’s promised subtle semantic difference: augmented assignment like x += y “takes the value” out of x and then sets x to null before calling + with the argument. To give a concrete example, this code successfully appends 1 to x but prints x is null:

x := [];
myappend := \a, b -> (
  print("x is", x);
  a append b
);
x myappend= 1;

This highly unusual behavior turns out to be really important for efficiency, but to explain why, I have to talk about Noulith’s curious semantics around immutability.

Immutability and copy-on-write semantics

Possibly the weirdest semantic feature of Noulith is its approach to immutability. In Noulith, all built-in data types are immutable, in the sense that the assignment to x in the following code doesn’t affect y and vice versa:

x := [1, 2, 3];
y := x;
x[0] = 4;
y[1] += 5;

The same principle applies if you pass x into a function. That function cannot mutate x through its parameter. However, as the same snippet demonstrates, variables holding lists are mutable, and you can set and mutate their elements individually.

To be perfectly honest, this “feature” is something I mostly sleepwalked into: Rust, the implementation language, is really big on immutability, and Rc<Vec<Obj>> is shorter than Rc<RefCell<Vec<Obj>>>. But in hindsight, there are plenty of reasons to like it:

• Nearly everybody who completes Advent of Code in Python learns that you can’t initialize a grid you intend to mutate later with code like x = [[0] * 10] * 10, because then x will consist of ten references to the same mutable list. An assignment like x[0][0] = 1 will set 1 in every row. Oops.

  

  Noulith avoids this pitfall.

• Because Python lists are mutable, they can’t be used as dictionary keys, so you need to use Python’s separate tuple type if you want to key a dictionary by sequences. This may mean a bunch of explicit conversions when accessing the dictionary. Noulith also dispenses with this.

The big, obvious downside is that, if this is implemented naively, mutation is slow! If every assignment like x[i][j] = k had to make a copy of the entire array in case some other variable refers to x, writing performant imperative code would become immensely difficult. I didn’t immediately consider this a dealbreaker — it’s possible to just suck it up and say that Noulith programmers have to get good at working with immutable data structures. As a parallel, you can write a lot of code in Haskell while staying firmly in the land of immutable data structures, generally by building new data structures in sweeps rather than individual mutations (though Haskell’s ecosystem has much more sophisticated data structures to support translating mutation-flavored algorithms, like the finger trees of Data.Sequence⁸, not to mention neat ways to achieve local mutability like with the ST monad). Another plausible escape hatch would have been to expose an explicit “mutable pointer” type.

However, none of that ended up mattering because it was far easier than I expected to implement this non-naively in Rust. The key is that Rust’s reference-counted pointer Rc lets you inspect the reference count and mutate through a pointer if and only if you hold the only pointer to that particular value — otherwise, you can choose to make a copy. In practice, you can just call Rc::make_mut. Thus, if you make an \(n \times n\) grid x := 0 .* n .* n and mutate a bunch of cells with x[i][j] = k, some rows will be copied in the first few mutations since their reference counts are > 1, but eventually every row will point to a unique list that can be safely mutated without copying, and the whole endeavor amortizes out to \(O(n^2)\) plus \(O(1)\) per assignment, exactly as asymptotically performant as it would be in, say, Python.

This behavior is the reason for the bizarre temporarily-stashing-null behavior of augmented assignment. Without it, when executing x append= y and calling the append function, there will always be another live reference to the list being appended to, which guarantees Noulith has to perform a \(\Theta(n)\) copy of the list and append to the copy, making append= unusably inefficient. But with this feature, in most common cases append can mutate x and get the job done in \(O(1)\) time. This wasn’t always the strategy: for a while, I kept the old value in x by default and manually marked a bunch of built-ins as pure so that the extra reference would be dropped only when one of those was the function used for augmented assignment. But eventually I decided manually marking built-ins as pure was too much work, too fragile, and still liable to miss cases where the extra reference could be dropped. In particular, it would prevent users from easily writing an efficient function like myappend for a custom data structure without a ton of additional language support. So I just enshrined this behavior into the semantics.

Why don’t other languages take this approach? I expect the answer is just that it’s “too magic”. Subtle changes in your code can easily leave an extra reference to a list somewhere and make manipulations much slower. Not all code is performance-critical, but preventing programmers from reasoning about performance locally to this extent is a big deal.

There are other aspects of Noulith where immutability is even more poorly thought out. The main thing is the presence of a handful of “lazy streams” that can execute arbitrary code when you iterate over them, similar to Python generators or lazy maps in other languages. In theory, it doesn’t make sense to copy a stream like that and pretend it’s immutable. The stream could be modifying files or sending packets as you iterate over it — you can’t just put it in two variables, iterate over one, and expect the other stream to still represent the same sequence of elements. In practice… well, you can just shrug, call it undefined behavior if the code isn’t a pure function, and allow the programmer to shoot themselves in the foot.

Other assignments and mutations

One of the less pleasing consequences of immutability is that there’s no way to call a function that will mutate an argument. This is unfortunate because there are plenty of common mutations you might want to perform on complex data structures, such as popping the last element from a list, that seem like they should be functions. There is no way to implement a normal function pop such that, if you have a list xs, calling pop(xs) modifies it. You might try to make do by making pop a function that takes a list and separately returns the last element and the list of all previous elements (this is an existing built-in, unsnoc — the inverse of snoc, the reverse of cons, as Lispers will recognize), and then asking people to write:

xs, (x:) = pop(xs)

But if you did this, while pop is running, xs will still refer to the list being popped, so pop will always have to inefficiently make a \(\Theta(n)\) copy of the list, just as append would have without our special handling around augmented assignment. This would make it essentially unusable.

So… I made pop a keyword that mutates its operand and returns the popped value.

There are two other keywords that perform similar mutations: remove removes an element from a list or a value from a dictionary, so given,

xs := [1, 2, 3, 4];

remove xs[1] will evaluate to 2 and will leave xs set as [1, 3, 4]. And consume is the lowest-level mutator that takes the value from an lvalue and leaves behind null, in a mechanism vaguely reminiscent of C++ move semantics. This at least gives you another way to efficiently pop an element if you only had unsnoc:

xs, (x:) = unsnoc(consume xs);

More importantly, this lets you write and use analogous efficient mutating functions for custom data structures, although it’s quite verbose. It may be worth introducing a keyword that more elegantly converts unsnoc to pop.

There are a few other weird assignment-related keywords. swap x, y swaps two lvalues, which I think I mostly put together just for the sake of making a good precedence demo. Here’s the remade screenshot from earlier:

The tiny advantage of the swap keyword over the classic Pythonic x, y = y, x is just that it’s more concise when the expressions being swapped are long, as they are in the screenshot.

And finally, the every keyword is a way to assign one expression to multiple variables or even at once, like so: every a, b, c = 1. In part, this is Noulith’s response to constructs like Python’s chained assignment a = b = c = 1, which I believe was itself a restricted version of assignments in a language like C. In C, expressions that evaluate to the assigned value and so can naturally be chained, but allowing this in full generality is a common source of bugs (consider the dreaded if (a = b) when if (a == b) was intended). However, every also walks through sliced lists and dictionaries, giving it a different set of powers than chained assignment. Assuming x is a list, code like every x[2:5] = 1 assigns 1 to each of x[2], x[3], and x[4]. I cannot remember if I had a specific use case or pain point in mind when designing every; it comes in useful once in a while, but so would a lot of features. I can, just barely, find one place I used it on 2016 Day 8. So it may be one of those things that sticks around purely through inertia.

Naming built-ins

Syntax is important [citation needed], but a language also needs built-in functions to, well, function.

Noulith has a lot of sequence-manipulating and higher-order functions with English names (map, filter, etc.) that I won’t discuss too much, except with respect to two recurring issues:

• What part of speech and tense should these function names be? For example, should the function that sorts a list — or more precisely, receives a list and returns a sorted copy — be called sort or sorted? One line of thought I recall from Java Puzzlers recommends the latter to describe functions that take an input and produce a new output instead of mutating the input, since the present-tense verb connotes mutation. I think this makes sense in contexts where both kinds of functions appear often, but immutability is so central to Noulith that I decided using shorter present-tense verbs would not cause any confusion.
• Should identifiers with multiple words be named with CamelCase or snake_case? This is a tough question that I’ve flipflopped on. Aesthetically, I think snake case looks better, but this is totally subjective; camel case is more compact and easier to type (word breaks marked by capital letters require hitting Shift one extra time, whereas the underscore itself requires Shift plus another key). I chose snake case for now mostly because both it’s standard in both Rust, the implementation language, and Python, the scripting language I’d previously use for most use cases Noulith was meant to target.

Arithmetic operators and semantics

A far more interesting topic is choosing the names and definitions of functions with symbolic names, the most familiar of which are the ones for performing basic arithmetic. It might be surprising how much inter-language variation there is here. I think the only uncontroversial operators are +, -⁹, and *.

• What does / mean? Probably division (though not in, e.g., J!), but what kind? In low- to medium-level languages it’s typical for / to mean integer division. It also used to do so in Python 2, but became float division in Python 3. I actually also used the float division definition at first, but eventually I realized that, because I really didn’t care about performance and wanted to do Real Math™, I might as well add rational numbers as in Common Lisp.¹⁰
• What does % mean? Probably remainder/modulo, but there are several subtly different semantics for it. (And again J has % mean division.) I ended up keeping the C-style behavior for % and offering the paired // and %% for rounding-down division and sign-of-divisor remainder.
• What does ^ mean? There is a bit of a schism here: mathematicians and a handful of programming languages (e.g. Haskell, Lua, Awk (!)) use it for exponentiation due to connoting a superscript and/or LaTeX influence, but lower-level languages usually use it for bitwise xor. I chose to side with the mathematicians here, because for my use cases, I expected exponentiation to be more practically useful than xor, so I didn’t want to give it a longer name like ** (plus, I thought there was a natural sequence-related definition for **).

• How are comparisons made? These are mostly uncontroversial. We do want = to mean assignment, so == is pretty locked-in, and < > <= >= are also close enough to universal¹¹ that I never seriously considered any alternatives (despite their mild conflict with augmented assignment), but the most common inequality operator != is harder to justify because ! does not mean “not” in Noulith. I considered Haskell’s /= (which visually looks more like ≠), but that would collide with the natural syntax for augmented division-assignment (an issue Haskell itself has experienced: the Lens operator //= uses a double slash for this reason, and, for consistency, so does every other division-related Lens operator). The alternative I found the most compelling was actually <>, prominent in SQL and offered in Python 2 all the way up until its dying gasp, which is actually quite internally consistent with the other comparisons. But in the end I thought the external consistency consideration for != was still overwhelming. Other languages that use != for not-equals without using standalone ! to mean “not” include OCaml and fish.

  I also included the three-valued comparison “spaceship operator”, <=>, as well as its inverse, >=<.

• What symbols should be used for bitwise operators? There are some real benefits to not assigning & and | and instead giving those symbols other purposes. For example, & could be saved for some type of concatenation (popular in spreadsheets), which I’d expect to use overwhelmingly more often in scripts than an operator for bitwise AND. But what would I call them instead? Haskell calls them .&. and .|. and F♯ calls them &&& and |||, but I couldn’t find any specific symbolic alternatives with convincing precedent. I think the main alternative would just be to give them a prose name like bitand/bitor instead. Eventually I decided to stick with & and | out of the additional consideration that it was more internally consistent if most operators for doing math on two numbers were single characters (though the paired division/modulo // and %%, as well as bit shifting << and >>, are all still two characters).

  But wait, given that I assigned ^ already, how do I write bitwise xor? I eventually realized that I could overload ~ to perform either bitwise complement or xor, depending on whether it’s called with one or two arguments; this is actually internally consistent with how we already decided - would work. Furthermore, this is the same approach as the numerical analysis language Yorick and, curiously, the exact mirror of Go’s approach, whereby ^ means both bitwise xor and complement so that ~ can be assigned a different meaning, so this decision isn’t indefensible in terms of external consistency either. I didn’t consciously recall these examples when deciding on these names, but felt like there was precedent.

Sequence operators

• What operator should we use for list and/or string concatenation? One of the most popular options is overloading +, but I never actually really liked that. I think overloading the same operator to mean numeric addition and sequence concatenation is really hard to justify from first principles. Nor is it satisfying to the mathematicians: any algebraist will tell you that + usually connotes that you’re working in an abelian group, but concatenation is neither commutative (in general, a + b does not equal b + a) nor invertible (in general, there is no “negative string” -a such that a + -a is the identity element, i.e., the empty sequence). Furthermore, you could imagine generalizing + and other arithmetic operators to some sequences, simply by adding or operating on elements pairwise, and in fact I did want to do that for the specific sequence type of “vectors” because it’s immensely useful in practice.

  So, what instead? There are a lot of options justifiable with precedent: D uses ~, some MLs and F♯ use @, Ada uses &, Smalltalk uses ,, Maple (and notation popular in cryptography) sometimes uses ||¹²… Eventually I went with Haskell/Scala’s ++ because it generalizes well to suggest symbolic names for other sequence operations, obtained by doubling similar arithmetic operators: ** is the Cartesian product; &&, ||, -- combine sets.

  Following this train of thought also allows us to define systematic operators for prepending/appending. Here Scala uses +: and :+, with the mnemonic, “the collection is on the colon side”, but I wanted to save the colon for other things, so I instead chose . with the opposite orientation, a single dot on the side with a single object. So .+ prepends one item to a list and +. appends one item to a list. This also generalizes well to other kinds of collections and operations: adding one element to a set can be |., “replicating” an item into a list of n items can be .*, joining two items into a length-2 list can be .., etc. One popular and pretty reasonable complaint about languages that make extensive use of operators or support operator overloading is that operators are particularly cryptic and hard to look up, so I wanted the “vocabulary” of operator symbols to be conceptually simple.

  I also chose to allocate a separate operator, $, to string concatenation, partly because I again thought the kinds of concatenation were conceptually distinct, partly because I could then make $ coerce all of its arguments to strings without feeling bad about shoehorning coercions into overloads. This became less compelling later as I added byte strings and “vectors” of numbers, which are other sequence types that sometimes need to be concatenated but that I didn’t want separate concatenation operators for, as well as format strings, which enable coercion to be done even more explicitly. Still, there’s something nice about having apply $ close at hand for mashing a bunch of strings together.

• Finally, this is not exactly an operator, but what syntax (if any) should we use for “splatting” — that is, declaring a function that takes a variable number of arguments and/or calling a function with a list of arguments? We can’t make * serve double duty as in Python/Ruby since it’s just a normal identifier, so ... of languages like JavaScript seemed the best idea.

More function composition

The last batch of operators I think are worth remarking on are those for function composition. I stole >>>, <<<, &&&, and *** from Haskell’s Control.Arrow:

(f <<< g <<< h)(a, b, c) = f(g(h(a, b, c)))
(f >>> g >>> h)(a, b, c) = h(g(f(a, b, c)))
(f &&& g &&& h)(a, b, c) = [f(a, b, c), g(a, b, c), h(a, b, c)]
(f *** g *** h)(a, b, c) = [f(a), g(b), h(c)]

They are quite verbose, but I couldn’t think of a better batch of names that would be acceptably internally consistent.

A slightly different function composition operator is Haskell’s on, which is actually from Data.Function, and primarily intended to be used in the exact same way.

(f on g)(a, b, c) = f(g(a), g(b), g(c))

Finally, lists of arguments can be “splatted” into functions with the JavaScript-inspired of and apply, which is useful for chaining with things that produce lists:

f of [a, b, c] = f(a, b, c)
[a, b, c] apply f = f(a, b, c)

Lessons learned

I think I predicted that requiring myself to use only Noulith on Advent of Code would make my median leaderboard performance better but my worst-case and average performances significantly worse. I don’t think my median performance improved, but my worst-case performance definitely got worse. Somehow it still didn’t matter and I placed top of the leaderboard anyway. (I will note that 2021’s second to fourth place all didn’t do 2022.)

One completely predictable issue: Debugging Noulith code is much harder because most programmers can be pretty confident that the root cause of a bug isn’t a bug in the language implementation. That assumption is not safe when you also wrote the language! For every bug I encountered, I had to consider whether the cause might have been in the couple dozen lines I had written for that day or in the 13,000 lines of Rust I had written over the prior few months. In the end, I don’t think I ever encountered any correctness bugs in the language while doing Advent of Code — that is, bugs where the language executed a program successfully but gave the wrong result — but that didn’t prevent me from considering such a hypothesis at several moments, so I was still substantially slower debugging. I did encounter a few bugs that caused errors where they shouldn’t have, as well as surprising interactions between features that I’m not sure count as bugs but suggest a flaw in the design somewhere: for example, on Day 21, I realized that the natural stringification of negative fractions like -1/2 cannot be evaled due to the same precedence issues as always. Not to mention quite a few correctness bugs in later days that I was just lucky enough to not hit before Christmas.

I was also not quite pessimistic enough about my Noulith interpreter simply being slow. There weren’t any days that became impossible, but there were several days where I believe I would have finished several minutes faster if I had just implemented the same algorithm in Python, whereas I expected maybe only one.

Taking a step back, the language design process was a lot of fun. One thing I enjoyed, which would be unrealistic in a more serious language, was the freedom to just add keywords willy-nilly (swap, literally, coalesce). Adding keywords to a language with production users tends to be a big deal for the simple reason that it breaks code using that word as an identifier (unless the keyword manages to be a “soft keyword” or something, but that just complicates the parser even more). Also naming things is hard in general. (Although it’s not a keyword per se, consider JavaScript’s globalThis and the dozens of rejected names.) This freedom also allowed me to avoid the temptation to add punctuation to the syntax: the set of usable punctuation characters is much more finite and makes me want to be quite confident that a language feature is worthy of one before assigning a character to it, not to mention that search engines often have trouble with documentation for them.

Reflecting on the entire process, strangely enough, I’m reminded of this bit from Lockhart’s Lament, about imagining and investigating mathematical objects:

[O]nce you have made your choices […] then your new creations do what they do, whether you like it or not. This is the amazing thing about making imaginary patterns: they talk back!

The language design and semantics, independent of the implementation, are in some sense an imaginary pattern, and I did often feel like the choices I made “talked back”. See how chaining comparison operators led to mutable runtime operator precedences, or how immutability led to a custom world of move-semantics-like keywords. Pretty neat.

As for my broader practical goals for Noulith, in terms of becoming a better go-to language for quick and dirty scripts: it worked, 100%. I solved at least two Mystery Hunt puzzles with it and used it extensively for data munging in another upcoming project, sometimes while I was on a different system without my dev setup, and I expect to continue.

Still, maybe the most generalizable takeaway is just how I encountered Hyrum’s Law. I haven’t made any promises of stability/compatibility in any shape or form — I haven’t updated the Cargo.toml version field from 0.1.0 since the first commit — but it sort of doesn’t matter anyway: there’s a bunch of random Noulith files out there in the wild, somebody even wrote a puzzle about the language, and I would feel a little bad for breaking them without a good reason.

Overall, 10/10, would do again.

The fun fact roulette

In no particular order, here are some fun facts about non-Noulith languages that I learned or remembered while writing this post. They’re all referenced somewhere in the 16,000 preceding words but I don’t blame anybody for not reading all that.

Did you know that:

• In Swift, operator precedences form a poset — an operator’s precedence can be greater than, less than, equal to, or incomparable with another’s?
• In Prolog, operators have precedences that are integers between 0 and 1200?
• In Game Maker Language, numbers are cast to booleans by checking if they’re greater than or equal to 0.5?
• In TLA⁺, the Cartesian product × is a special syntax construct rather than an infix operator so that n-way Cartesian products hold n-tuples rather than nested pairs?
• In Ceylon, variables are declared to be mutable with the eight-letter keyword variable?
• More than three dozen names were rejected for JavaScript’s globalThis?
• In Haskell, the - prefix operator is syntactically special and always calls the default (Prelude) negate function, regardless of whether the default - and negate are in scope?
• In LiveScript, the operators <? and >? compute the min and max of their operands?
• An extremely rare breaking change to redefine range loop variables in each iteration is under consideration for Go 2?
• In Java, -2147483648 is a legal expression, but -(2147483648) is a compile-time error?

Appendix: What is a noulith?

Nouliths are the weapons wielded by Sages, a healer class from the critically acclaimed MMORPG Final Fantasy XIV, with an expanded free trial in which you can — *ahem*

It is hard to describe exactly what nouliths are, but in-game we’re introduced to them as a set of four “short staves” that sages control with their mind to draw. A Wikipedia blurb calls them “magical aether foci”. According to Reddit sleuths, etymologically, the name is based on Ancient Greek: νόος “mind” + λίθος “stone”. (The Sage’s skill set is Ancient Greek and themed around the medical theory of Humors.)

I thought the name was apt because computers are also just smart rocks we try to control with our minds sometimes, and this programming language was an attempt to make a tiny corner of that control a little smoother for a single person. (Who also mains Sage nowadays.)