🅿️🅿️🅿️ordle

Don’t you hate it when CTFs happen faster than you can write them up? This is probably the only PlaidCTF challenge I get to, unfortunately.¹

Web is out, retro is in. Play your favorite word game from the comfort of your terminal!

It’s a terminal Wordle client!

I only solved the first half of this challenge. The two halves seem to be unrelated though. (Nobody solved the second half during the CTF.) The challenge was quite big code-wise, with more than a dozen files, so it’s hard to replicate the experience in a post like this, but here’s an attempt.

There are four Wordle “levels”. To play the game, the client picks a level, makes a TLS connection to the server using some bundled certificates, and then sends guesses. The server responds to each guess with an “indicator”: a sequence of black, yellow, and green emoji. When the client guesses the word correctly, the server creates and sends a TLS certificate to it, and the client can present that certificate on a future connection to connect to the next level.

We are provided with the source code for the client and the server, including the word lists and some other assets, as well as a bunch of dev certificates for local testing; we’re only missing the private key for the server’s root certificate (and, of course, the real flag).

Level 1 is classic Wordle (albeit with answers drawn from a much worse word list). However, in Level 2 (which gives the first flag when solved), the “secret word” is a sequence of five random emojis drawn with replacement from a list of 236 emojis, for 732,082,482,176 possible answers; and you still only get six guesses. It’s not that obvious how to bound the probability of success if you play optimally, but a quick calculation to guide your intuition is that if you guess 25 distinct emoji for your first five guesses, the probability that all five answer emoji are among those guesses is around 0.001%. Connecting to the server also includes a delay, so brute force is not really an option here.

Is there any other way to figure out the answer emoji? Let’s look at how they’re generated:

func emojiGenerator() (word []rune, attempts int) {
    for i := 0; i < 5; i++ {
        word = append(word, unicode.ToUpper(level2Emojis[rand.Intn(len(level2Emojis))]))
    }
    return word, 6
}

The rand here is "math/rand", which is enough to raise some eyebrows. The challenge contains a lot of other certificate management code that also uses random numbers, but the other code conspicuously imports "crypto/rand", from which one can infer that "math/rand" is likely not cryptographically secure even without knowing anything about Go. Indeed, the math/rand documentation says:

Package rand implements pseudo-random number generators unsuitable for security-sensitive work.

…

This package’s outputs might be easily predictable regardless of how it’s seeded. For random numbers suitable for security-sensitive work, see the crypto/rand package.

The default Go Source for math/rand actually isn’t seeded at all, so it’s completely deterministic! Unfortunately, the server does seed it with the current time:

func init() {
    rand.Seed(time.Now().UnixMilli())
}

Still, this is not that hard to predict. The CTF is only 24 hours long, so assuming the server’s clock is not wildly out of sync and that it started during the CTF, there are only 86,400,000 possible seeds. That’s already a lot less than 732,082,482,176.

Another thing we can do is play games of 🅿️🅿️🅿️ordle Level 1, which shares its random number generator state with Level 2, and get information about the RNG state that way. This at least lets us do some amount of “local brute forcing” for the possible seed. However, if there is a smart way to derive the RNG state from a few samples mathematically (rather than just trying all states), I couldn’t see it. Our samples can at best tell us the seed modulo that length at some point in time, but the word list’s length is not a nice number, so it’s not clear how to use this information.

Still, these insights were enough for me to write a prototype where I started a local server and guessed the word just from the approximate time and some Level 1 solutions. Unfortunately, the seed isn’t the only unpredictable piece of information we need; on the real server, the RNG seed is constantly advanced by all the other teams trying to solve the challenge.

Is the state space still usefully bounded? As of time of writing, Go’s default math/rand RNG is not well-documented, but between a GitHub issue with some links and the source code, it appears that the state space is a somewhat ridiculous 2^64×607 ≈ 10^11,694. That is, shall we say, the opposite of less than 732,082,482,176. Ultimately, thinking about the state space as (initial seed) × (number of times the RNG has been advanced) still produces more reasonable bounds. To make up some numbers: Say we manage to catch the server within an hour of its restart, and that other teams have advanced the RNG at most 10,000 times. Then the number of RNG states we have to consider is 36,000,000,000. That’s a little less than 732,082,482,176, but it’s still well out of reach of brute force.

How else can we reduce the search space?

What time is it?

One question I found useful to step back and contemplate is simply: why does the challenge have such an absurd amount of infrastructure for making and verifying SSL certificates? Surely there are simpler ways for a server to give clients something they can later use to prove they solved a level. Maybe we can use the server certificate somehow?

Let’s look at a certificate. Here’s the one for this blog, at least when I was writing this post.

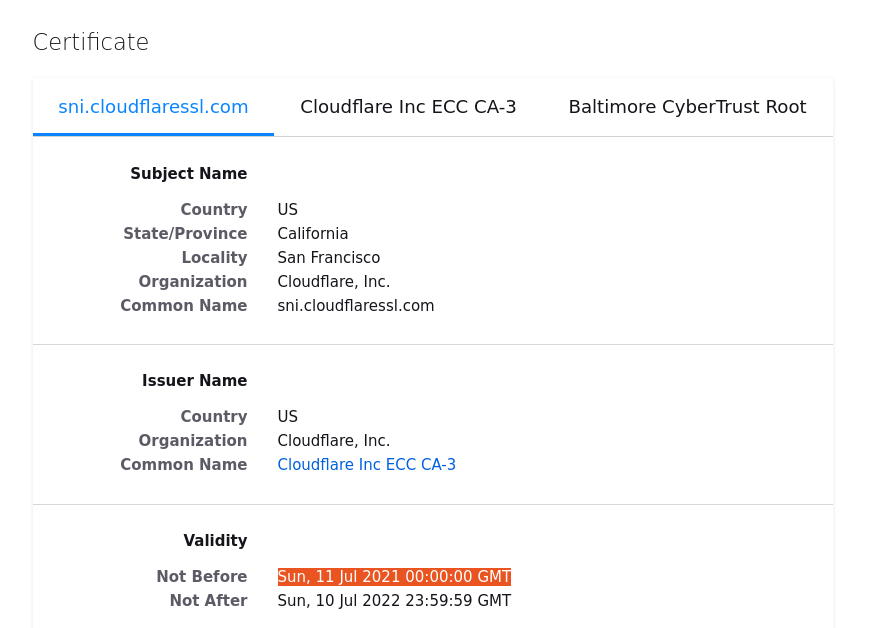
SSL certificates has timestamps. What timestamp does the server put in its certificates, and when?

Turns out, it’s actually time.Now(), exactly the same expression used to seed the RNG!

cert := &x509.Certificate{
    SerialNumber: config.Serial,
    Subject: pkix.Name{
        Country:      []string{"🇺🇸"},
        Province:     []string{"Pennsylvania"},
        Locality:     []string{"Pittsburgh"},
        Organization: []string{"PlaidCTF"},
        CommonName:   config.CommonName,
    },
    DNSNames:              config.DNSNames,
    NotBefore:             time.Now(),
    NotAfter:              time.Now().Add(time.Second * time.Duration(config.SecsValid)),
    IsCA:                  config.Parent == nil,
    KeyUsage:              keyUsage,
    ExtKeyUsage:           extKeyUsage,
    BasicConstraintsValid: true,
}

Well, not exactly exactly, because we only get the time down to a granularity of one second. But by looking at the server, and adding one second of leeway on both sides just to not worry about it, we can narrow down the set of seeds to 3,000.

Suddenly the numbers are looking feasible!

We can lightly modify the client to print out the server certificate’s NotBefore timestamp:

conn, err := tls.Dial("tcp", sessionServer, tlsConfig)
log.Println(len(conn.ConnectionState().PeerCertificates))
for i, c := range(conn.ConnectionState().PeerCertificates) {
    log.Println(i, c.NotBefore.UnixMilli())
}

I think there is a lot of flexibility in how to solve the challenge from here. Another useful observation for effectively narrowing down possible RNG states is that the server samples the secret word and advances the RNG when you connect, so if you start two connections quickly one after another, you have a good chance of sampling two adjacent RNG states. Because I wasn’t very fluent in Go, I went about this in a really hacky way and didn’t automate too much of the process. I did hack in one keyboard shortcut to quickly submit an isogrammatic triplet of words, but otherwise, I solved Wordles manually and pasted numbers between Go scripts running in different terminals. Here’s what I did:

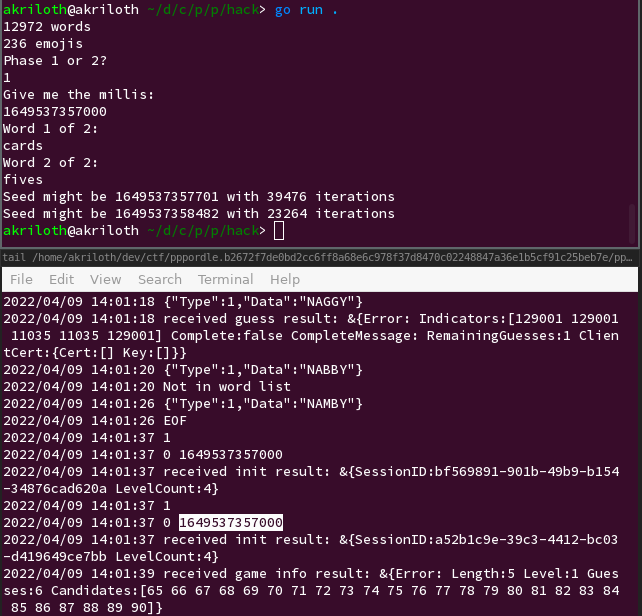
1. Start two connections to the server Level 1, as quickly in succession as humanly possible.

2. Solve both Wordles.

   

   This is not easy because there’s a one-minute time limit (during which you have to solve both) and the answer isn’t revealed if you fail. I think it’s hilarious that speed-solving Wordles turned out to be a useful skill here. (Obviously I could have scripted this, in a separate script that I manually interacted with if necessary — but where’s the fun in that?)

3. Look at the client logs to extract the NotBefore timestamp. Using brute force, look for seeds near the timestamp and numbers of iterations that would cause those two words to be sampled.

   

   As in the above example, doing this step once is often not enough to uniquely identify the seed, and there’s always a risk that you don’t manage to catch two adjacent seeds in step 1.

4. Repeat steps 1 to 3 until you are confident about the seed, and while the server NotBefore timestamp doesn’t change. Usually seeing a particular seed twice is enough to be confident in it.

5. Start two connections to the server Level 1 and Level 2, as quickly in succession as humanly possible.

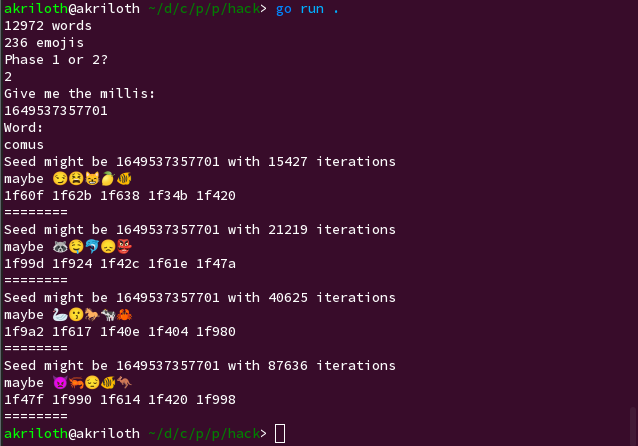
   Solve the first Wordle, then brute force a number of iterations that would cause that word to be sampled and submit the emoji sequence that would be generated from the next iteration. (In the below example, we picked the iteration count of 40625 as the first one after the iteration count we got from Step 3, 39476 iterations. Also, since I was on Ubuntu, I manually typed in each emoji using Ctrl-Shift-U, then the Unicode codepoint in hex, then Enter; there are surely better ways to do it for anybody more comfortable tinkering with the Go client.)

   

   

And we have the flag!

PCTF{L3@KY_S33D5_GR0W_INT0_B1G_PR0BL3M5}

For completeness, my solve script follows:

package main

import (
    _ "embed"
    "strings"
    "bytes"
    "math/rand"
    "log"
    "bufio"
    "fmt"
    "os"
    "strconv"
)

//go:embed level1_wordlist.txt
var level1WordlistBytes []byte

//go:embed level2_emojis.txt
var level2ValidEmojis string

func main() {
    reader := bufio.NewReader(os.Stdin)

    var level1Wordlist [][]rune

    scanner := bufio.NewScanner(bytes.NewReader(level1WordlistBytes))
    for scanner.Scan() {
        level1Wordlist = append(level1Wordlist, []rune(scanner.Text()))
    }

    if err := scanner.Err(); err != nil {
        log.Fatal(err)
    }

    level2Emojis := []rune(level2ValidEmojis)
    fmt.Println(len(level1Wordlist), "words")
    fmt.Println(len(level2Emojis), "emojis")

    fmt.Println("Phase 1 or 2?")
    prompt, _ := reader.ReadString('\n')
    for prompt[0] != '1' && prompt[0] != '2' {
        prompt, _ = reader.ReadString('\n')
    }

    fmt.Println("Give me the millis:")
    ms, _ := reader.ReadString('\n')
    ms = strings.TrimSpace(ms)
    millis, err := strconv.Atoi(ms)
    if err != nil {
        panic(err)
    }

    if prompt[0] == '1' {
        fmt.Println("Word 1 of 2:")
        word1, _ := reader.ReadString('\n')
        word1 = strings.TrimSpace(word1)
        fmt.Println("Word 2 of 2:")
        word2, _ := reader.ReadString('\n')
        word2 = strings.TrimSpace(word2)

        for m := millis - 1000; m < millis + 2000; m++ {
            r := rand.New(rand.NewSource(int64(m)))
            gen1 := string(level1Wordlist[r.Intn(len(level1Wordlist))])
            gen2 := string(level1Wordlist[r.Intn(len(level1Wordlist))])
            for its := 0; its < 100000; its += 1 {
                if gen1 == word1 && gen2 == word2 {
                    fmt.Println("Seed might be", m, "with", its, "iterations")
                }
                gen1 = gen2
                gen2 = string(level1Wordlist[r.Intn(len(level1Wordlist))])
            }
        }
    } else {
        fmt.Println("Word:")

        word1, _ := reader.ReadString('\n')
        word1 = strings.TrimSpace(word1)

        r := rand.New(rand.NewSource(int64(millis)))
        gen1 := string(level1Wordlist[r.Intn(len(level1Wordlist))])
        for its := 0; its < 100000; its += 1 {
            if gen1 == word1 {
                fmt.Println("Seed might be", millis, "with", its, "iterations")
                var guess []rune
                for i := 0; i < 5; i++ {
                    guess = append(guess, level2Emojis[r.Intn(len(level2Emojis))])
                }
                fmt.Println("maybe", string(guess))
                fmt.Printf("%x %x %x %x %x\n", guess[0], guess[1], guess[2], guess[3], guess[4])
                fmt.Println("========")
            }
            gen1 = string(level1Wordlist[r.Intn(len(level1Wordlist))])
        }
    }
}